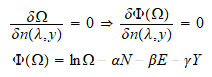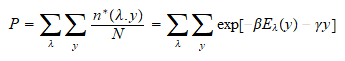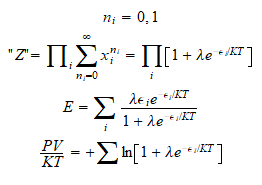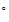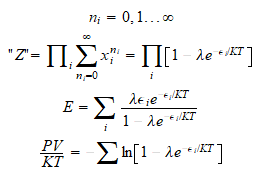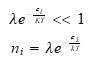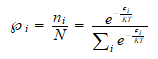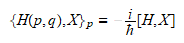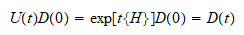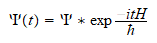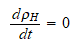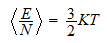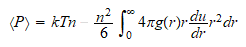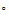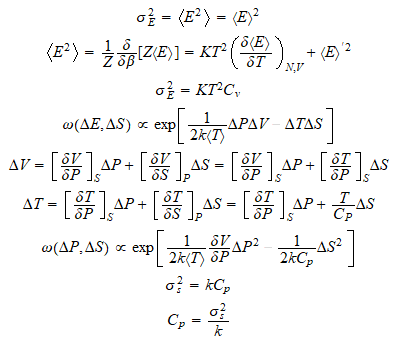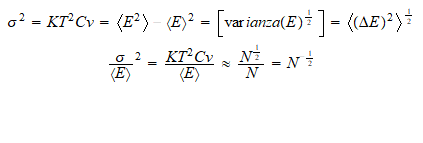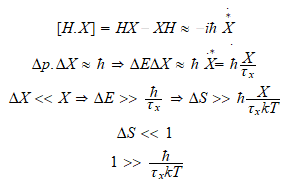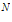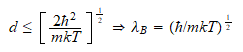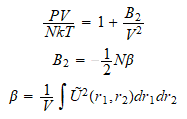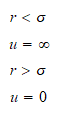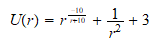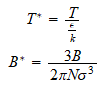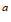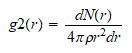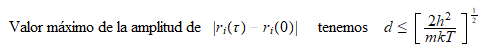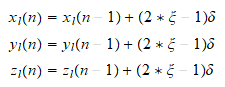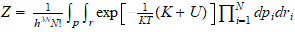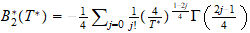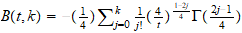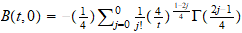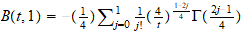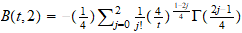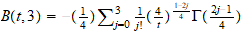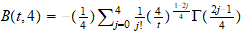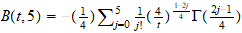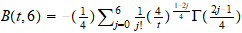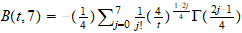http://schemas.microsoft.com/office/word/2003/wordml2450
OBJETIVOS Y METODOS DE LA TERMODINÁMICA
ESTADÍSTICA.Futuros colegas:
Este curso trata de Termodinámica Estadística (Mecánica
Estadística) que hace de puente de unión entre la teoría
cuántica y la termodinámica (y ya veréis mas adelante que se
puede decir que la mecánica cuántica y la mecánica
cuántica estadística son correspondientes, sufriendo un desfase
entre ellas de pi/2 respecto al eje imaginario z).
Subrayaremos los
puntos de especial interés. Y vamos primeramente a formaros con una parte
puramente teórica, "Fundamentos" para
pasar a una segunda parte que trata de las
"Aplicaciones".
Fundamentos: los
vamos a estructurar de la siguiente forma:
Temas 1 y 2
El formalismo
de colectivos es un artificio teórico que nos permite promediar
propiedades de un sistema sobre todos los estados cuánticos posibles,
Pues intuimos que hacer el promedio temporal o el promedio sobre
sistemas
en un t dado, para obtener una propiedad F es equivalente.
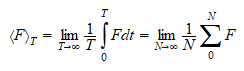 Demostraremos
que de todas las distribuciones posibles solo una, la máxima (que nos
permitirá aplicar la condición de máximo) contribuye
apreciablemente en el calculo de propiedades macroscópicas. De ese modo,
se van a determinar los números de ocupación (los cuales definen la
distribución) y, consiguientemente, la probabilidad de que un sistema
posea un valor de la energía y de los parámetros-y, a través de
la condición de máximo (aplicando la técnica de los
multiplicadores de Lagrange y utilizando la aproximación de Stirling).
Demostraremos
que de todas las distribuciones posibles solo una, la máxima (que nos
permitirá aplicar la condición de máximo) contribuye
apreciablemente en el calculo de propiedades macroscópicas. De ese modo,
se van a determinar los números de ocupación (los cuales definen la
distribución) y, consiguientemente, la probabilidad de que un sistema
posea un valor de la energía y de los parámetros-y, a través de
la condición de máximo (aplicando la técnica de los
multiplicadores de Lagrange y utilizando la aproximación de Stirling).
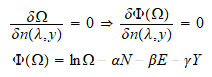 A partir de ese punto (y al comparar los resultados con la termodinámica
fenomenológica) se define la entropía en términos
estadísticos y se está en condiciones de establecer expresiones de
las propiedades termodinámicas en función de magnitudes
microscópicas.
A partir de ese punto (y al comparar los resultados con la termodinámica
fenomenológica) se define la entropía en términos
estadísticos y se está en condiciones de establecer expresiones de
las propiedades termodinámicas en función de magnitudes
microscópicas.
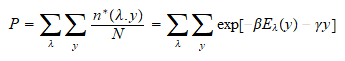 Obtenemos
funciones de partición para sistemas interactuantes, deduciéndose
con posterioridad como caso particular el sistema ideal (no
interacción)
Obtenemos
funciones de partición para sistemas interactuantes, deduciéndose
con posterioridad como caso particular el sistema ideal (no
interacción)
Y veremos las diferencias entre las distribuciones de
Fermi-Dirac, Bose- Eintein, Maxwell-Boltzman (clásica/semiclasica).
En los fermiones se cumple el principio de exclusión de Pauli y no
puede haber dos en el mismo nivel cuantico con lo cual la función de
partición macrocanonica es;
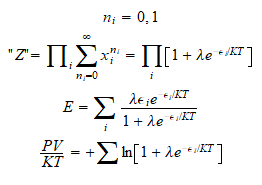 Sin embargo en el caso de los bosones no hay restricción al
n
Sin embargo en el caso de los bosones no hay restricción al
n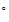 de partículas que ocupan el mismo nivel
de partículas que ocupan el mismo nivel
energético con lo cual:
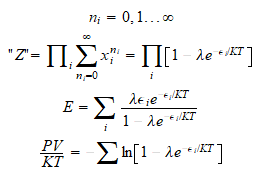 La estadística de Maxwell-Boltzman es una simplificación de las
anteriores, ya que en el limite clásico suponemos muchos más niveles
que partículas y por tanto el factor que diferencia a la estadística
de Fermi --Dirac o Bosse-Einstein.
La estadística de Maxwell-Boltzman es una simplificación de las
anteriores, ya que en el limite clásico suponemos muchos más niveles
que partículas y por tanto el factor que diferencia a la estadística
de Fermi --Dirac o Bosse-Einstein.
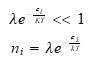 Y por tanto al ser despreciable frente a 1 nos queda:
Y por tanto al ser despreciable frente a 1 nos queda:
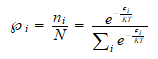
Temas 3 y 4 Hecho esto se aborda a continuación el
planteamiento de un formalismo extraordinariamente poderoso y paralelo al de
funciones de partición. Nos referimos al de funciones de
distribución, que aplicaremos al estudio del equilibrio de sistemas que
admiten una descripción clásica, estribando su interes en que son
aplicables a situaciones de no equilibrio.
El principio de correspondencia asocia a cada corchete de Poisson un
conmutador de Heinsenberg.
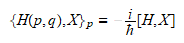 Veremos
que a través del propagador u operador de Green conocida la función
en un punto del espacio fásico conoceremos su evolución a
través del tiempo. Llegamos pues a un determinismo en el desplazamiento
temporal.
Veremos
que a través del propagador u operador de Green conocida la función
en un punto del espacio fásico conoceremos su evolución a
través del tiempo. Llegamos pues a un determinismo en el desplazamiento
temporal.
Los corchetes de Poisson (que son un caso concreto de los
corchetes de Lie) generan la entidad que se llama
propagador\nobreakspace u
operador de Green U(t) que cumple:
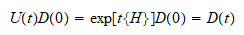 Produciéndose
un automorfismo\nobreakspace
de D(0) en
D(t)\nobreakspace
generándose un grupo continuo (grupo de Lie). Podemos asimilar la
actuación de U(t) sobre D(0) como si se tratara de un desplazamiento
temporal.
Produciéndose
un automorfismo\nobreakspace
de D(0) en
D(t)\nobreakspace
generándose un grupo continuo (grupo de Lie). Podemos asimilar la
actuación de U(t) sobre D(0) como si se tratara de un desplazamiento
temporal.
No solo hay cierta similitud entre los corchetes de Poisson y
los conmutadores de Heisenberg sino también entre los operadores de Green
y los de evolución temporal cuánticos sobre
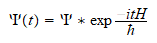 Os
recordamos ahora que en el primer capitulo hablábamos del determinismo
temporal cuántico con la Ecuación de Liouville-von Neumann.
Os
recordamos ahora que en el primer capitulo hablábamos del determinismo
temporal cuántico con la Ecuación de Liouville-von Neumann.
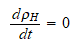 \nobreakspace Veremos como
a través de las funciones reducidas llegaremos a la expresión (para
el caso ideal),
\nobreakspace Veremos como
a través de las funciones reducidas llegaremos a la expresión (para
el caso ideal),
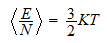 Idéntica
a la que llegábamos a través de las funciones de partición. Lo
que prueba la fiabilidad de ambos sistemas.
Idéntica
a la que llegábamos a través de las funciones de partición. Lo
que prueba la fiabilidad de ambos sistemas.
El valor de una variable
intensiva depende de su entorno local. Incluso en estado no estacionarios los
respectivos gradientes definirán el valor de la variable intensiva en
cualquier punto. A todo aquello lo llamamos principio de equivalencia
microscópica y a través de esta definiremos el paso al limite
termodinámico como el valor que adquieren las variables intensivas cuando
las extensivas tienden a
infinito.
La utilidad del limite
termodinámico es que prescindimos de fenómenos superficiales y que
se puede trabajar con un numero de partículas y un volumen cualquiera
pues admitiremos que una variable intensiva no depende del volumen escogido
aunque la densidad siempre será constante.
Ecuación de estado de presión media (presuponiendo aditividad par en
las interacciones). A la ultima parte del segundo termino lo llamamos del
virial.
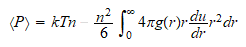 Y
a través de las fluctuaciones en
n
Y
a través de las fluctuaciones en
n de partículas llegaremos a la ecuación de estado de compresibilidad:
de partículas llegaremos a la ecuación de estado de compresibilidad:
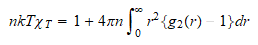 Que
es una variante de la función de estado pues nos relaciona la
variación de la presión con la función g2.
Que
es una variante de la función de estado pues nos relaciona la
variación de la presión con la función g2.
El
3 principio de la termodinámica es consecuencia de la Mecánica
Cuántica. ya que de el se deduce que solo podemos conocer la
variación de S y no su valor absoluto ( algo que se tuvo que admitir ya
en la termodinámica como en la Mecánica Estadística).
principio de la termodinámica es consecuencia de la Mecánica
Cuántica. ya que de el se deduce que solo podemos conocer la
variación de S y no su valor absoluto ( algo que se tuvo que admitir ya
en la termodinámica como en la Mecánica Estadística).
Tema 5
El estudio de fluctuaciones, trata de que un valor nos viene definido por una
distribución de valores centrado en lo que consideramos el valor medio de
esta oscilación. Dependen parámetros tan importante como Cv, Cp..
Cp se puede interpretar como la precisión con que se puede medir la
entropía y Cv como la precisión de la energía.
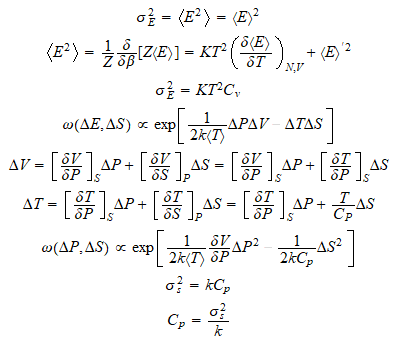 Los sistemas con Cv grande son propensos a acumular energía
robándola de su entorno a través de las fluctuaciones.
Los sistemas con Cv grande son propensos a acumular energía
robándola de su entorno a través de las fluctuaciones.
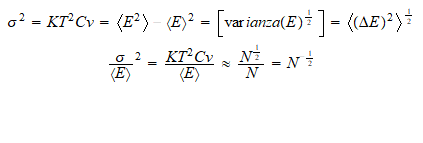 Para obtener el limite entre las fluctuaciones termodinámicas y
cuánticas, vamos a hacer una aproximación cuasi-clasica.
Para obtener el limite entre las fluctuaciones termodinámicas y
cuánticas, vamos a hacer una aproximación cuasi-clasica.
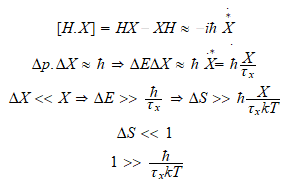 (comparar incremento KT con incremento de E entre niveles cuanticos).
(comparar incremento KT con incremento de E entre niveles cuanticos).
Vemos que podemos discernir entre fluctuaciones termodinámicas y
cuánticas Temperaturas muy bajas y tiempo de variación pequeño
implicaría fluctuaciones cuanticas.
En el tema 6 vamos a comparar KT con incremento de E entre niveles
cuanticos.
El
n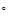 de estados cuanticos, es enorme del orden de
10
de estados cuanticos, es enorme del orden de
10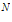 . Luego por muy pequeño que sea el incremento de E, habrá muchos
niveles disponibles.
. Luego por muy pequeño que sea el incremento de E, habrá muchos
niveles disponibles.
En el tema 10 al estudiar la integral sobre caminos (phat-integral) en la
aplicación Monte Carlo a líquidos que por su naturaleza (poco peso
molecular) o estado (temperatura baja) tengan un comportamiento cuántico
nos vendra determinado por el valor del diámetro de las cadenas y al cual
llegaremos a traves de un intricado mecanismo matematico, de curiosa
concordancia con la longitud de onda térmica de De broglie.
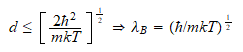 (hablar sobre lamda de De Broglie con dimensiones significativas del sistema).
(hablar sobre lamda de De Broglie con dimensiones significativas del sistema).
Tema 6
En el caso de temperaturas bajas, particulas ligeras etc., podemos necesitar
hacer un estudio cuantico del sistema, puede ocurrir que el sistema este
definido por un estado puro, en la menor de las veces, o bien que este
descrito por un estado mezcla, en este caso tendremos que definir y utilizar
el operador o matriz densidad.
Llegamos asi a la segunda parte, con ``Aplicaciones'' de interes Quimico que
estructuraremos de la siguiente forma;
Tema 7
El comportamiento real que se observa para un gas deberá ser una
consecuencia del incumplimiento de las limitaciones impuestas a priori para el
modelo ideal es decir las partículas no son puntuales y interaccionan
entre sí. Un estudio detallado de los gases reales debe hacerse teniendo
presentes dos puntos fundamentales: (i) cuál es su geometría
molecular y (ii) cuál es la descripción más precisa posible de
las interacciones entre moléculas.
Nos ceñiremos en aquellas
que aunque puntuales si presentan interacción para estudiar lo que
definiremos como ``enjambres'', siendo irreducibles aquellos que no tienen
ningún punto de articulación.
Veremos que tras un desarrollo en
serie de Taylor, los coeficientes del desarrollo coinciden con estos
enjambres. Obteniendo por tanto la relación entre la ecuación del
viriál y las interacciones moleculares.
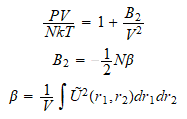 En los ejercicios veremos entre otros ejemplos importantes, cómo se llega
a ecuaciones tipo Wan dear Wals.
En los ejercicios veremos entre otros ejemplos importantes, cómo se llega
a ecuaciones tipo Wan dear Wals.
El potencial de esferas rígidas es
un modelo que considera a la partícula, rodeada de una esfera
impenetrable, mientras que mantenido entre ellas una distancia 2*gamma, pueden
moverse libremente.
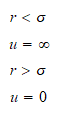 Sin embargo el potencial Lennard-Jones es mucho más realista
correspondiendo a la suma algebraica de un termino atractivo y otro repulsivo,
creando una curva con un valle de potencial al que tenderán las
partículas.
Sin embargo el potencial Lennard-Jones es mucho más realista
correspondiendo a la suma algebraica de un termino atractivo y otro repulsivo,
creando una curva con un valle de potencial al que tenderán las
partículas.
Queremos proponer, en esta prueba de ensayo, sobre la
conveniencia a nuestro parecer, de crear potenciales continuos, como por
ejemplo el caso de que el exponente sea función de la distancia, como si
el fenómeno de atracción, no tuviese que ver con fenómenos
particulares como repulsión entre nubes
electrónicas, etc., sino
que se correspondiese con un único fenómeno universal y continuado
de interacción entre la materia. Un ejemplo de potencial que se aproxima
bien a los conocidos seria;
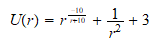 Independientemente de los motivos conceptuales por los que hemos llegado a
ellos, si funcionan deberemos admitirlos.
Independientemente de los motivos conceptuales por los que hemos llegado a
ellos, si funcionan deberemos admitirlos.
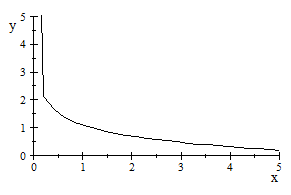
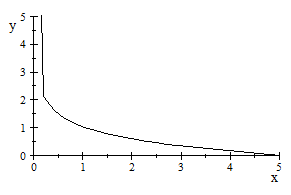
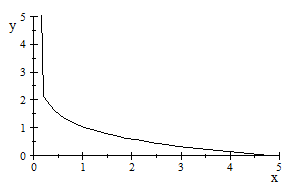
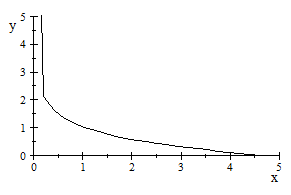
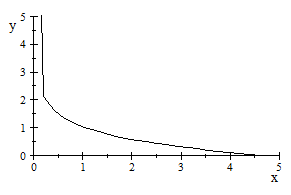
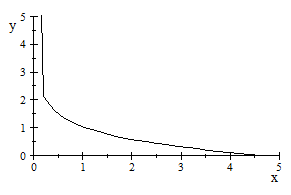
A través de planteamientos
moleculares. Encontramos en este capitulo, la posibilidad de programar por
integración numérica, aunque a través del Scientific Notebook
hemos podido representar la ecuación del coeficiente del
2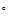 coeficiente del virial reducido
B
coeficiente del virial reducido
B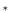 (T
(T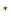 )
y hemos observado que el coeficiente j apenas influye a partir de 7 (ver
virial.tex).
)
y hemos observado que el coeficiente j apenas influye a partir de 7 (ver
virial.tex).
1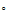 )
B2LJ.FOR: Permite calcular el segundo coeficiente del virial usando como
potencial intermolecular el de
Lennard-Jones.
)
B2LJ.FOR: Permite calcular el segundo coeficiente del virial usando como
potencial intermolecular el de
Lennard-Jones.
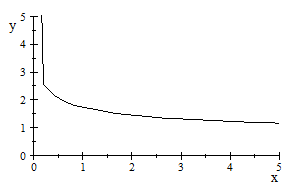
2 ) VlRIAL2.BAS: Permite hallar la curva que relaciona el segundo coeficiente
del viriál reducido con las temperaturas
reducida.
) VlRIAL2.BAS: Permite hallar la curva que relaciona el segundo coeficiente
del viriál reducido con las temperaturas
reducida.
3 )
PARFOT.FOR: Permite determinar los parámetros del potencial de
Lennard-Jones (potencial mínimo ypsilon y el radio a potencial cero
sigma)... mediante el ajuste de datos experimentales del segundo coeficiente
del virial (temperaturas y coeficientes del
viral).
)
PARFOT.FOR: Permite determinar los parámetros del potencial de
Lennard-Jones (potencial mínimo ypsilon y el radio a potencial cero
sigma)... mediante el ajuste de datos experimentales del segundo coeficiente
del virial (temperaturas y coeficientes del
viral).
4 )
V.BAS: Programa inspirado en virial2.bas que hemos preparado para esta prueba
de ensayo en principio genera los valores que relacionan
B
)
V.BAS: Programa inspirado en virial2.bas que hemos preparado para esta prueba
de ensayo en principio genera los valores que relacionan
B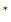 con
T
con
T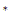 ,
luego al introducir un valor de B o T y a través de un tanteo aleatorio
busca el valor mas próximo a ypsilon y sigma.
,
luego al introducir un valor de B o T y a través de un tanteo aleatorio
busca el valor mas próximo a ypsilon y sigma.
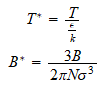 En este tema sobre gases reales llegaremos también a deducir la
función
analíticamente.
En este tema sobre gases reales llegaremos también a deducir la
función
analíticamente.
5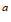 )
BUCMAX.BAS: Nos permitira eliminar de la integración, el intervalo en que
la el poterncial de Buckingham se comporta ``extrañamente''.
)
BUCMAX.BAS: Nos permitira eliminar de la integración, el intervalo en que
la el poterncial de Buckingham se comporta ``extrañamente''.
Temas 8-9-10
Estado liquido, cuyos contenidos están orientados la
simulación Monte Carlo
de líquidos clásicos y
cuánticos. Comentar que las moléculas de un liquido están
sometidas a una interacción muy fuerte (gran interactividad entre las
partículas).
Hasta ahora nos habíamos conformado en el estudio de los gases reales con
hacer un desarrollo de Taylor y coger los primeros términos, aquí en
los líquidos este sistema no sirve para simplificar, en consecuencia la
función de partición no admite factorización o es de muy
difícil factorización, todo nos conduce a estudiar un liquido a
través de sus funciones de partición, pero reducidas (ver3.2)
Funciones de distribución reducidas... funciones de correlación
(3.6)... de perturbaciones. Interacciones de muchos cuerpos..
En este tema
aprenderemos que dentro de las técnicas estocásticas,
aproximación gaussiana, calculo numérico, etc., se a comprobado
últimamente la efectividad del método Monte Carlo que da excelentes
resultados.
Estructura de un liquido g2 y su medida experimental (factor
de estructura).
De las funciones de correlación la más sencilla
y la única accesible es la función radial g2(r), que en el caso
habitual tridimensional seria.
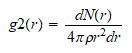 Aunque
estudiaremos tres tipos de determinación teórica de g2(r),
normalmente utilizaremos el método Monte Carlo donde promediaremos los
resultados obtenidos para cada ``partícula''.
Aunque
estudiaremos tres tipos de determinación teórica de g2(r),
normalmente utilizaremos el método Monte Carlo donde promediaremos los
resultados obtenidos para cada ``partícula''.
A través de la
función radial g(2) podemos deducir la presión del liquido, y
también la energía interna, aunque si utilizamos el potencial de
esferas rígidas la energía potencial va a ser cero y la energía
interna coincidirá con la cinética, si utilizásemos otros
potenciales como por ejemplo el de Lennard-Jones, si que obtendríamos
energía potencial, aunque habrá que hacerse cargo de resultados solo
aproximados.
Al admitir que las partículas pueden salir de su intervalo y otras entrar
en él, admitimos una serie indefinida-infinita de intervalos, de forma
que igual nos da el primero como el ultimo que podemos considerar relacionados
en forma cíclica,
Así unas celdas bidimensionales se
cerrarían primeramente formando un cilindro y este a su vez se cierra
formando un toro. Por ello el llamales toroidales.
Para un sistema
tridimensional seria un hipertoro que habría que representarlo en 4
dimensiones.
Descripción somera de como se procede en el método
Monte Carlo.
Con el método Metrópolis haremos que a través
de una cadena de Markov que definiremos como a=(2*ypsilon-1)*lamda
b=(2*ypsilon-1)*lamda y en donde asociaremos a ypsilon un
n aleatorio y lamda por tanteo haremos que produzca igual
n
aleatorio y lamda por tanteo haremos que produzca igual
n de intersecciones que de configuraciones sin intersección.
de intersecciones que de configuraciones sin intersección.
Hay
líquidos que no cumplen la ley de los estados correspondientes debido a
tener una longitud de onda térmica de De Broglie comparable con sus
distancias intraatómicas, es decir poco peso atomico/molecular o baja
temperatura.
Sustancias como el Helio liquido se escapan fuertemente de
dicho comportamiento así como el Neón en menor cuantía así
pues aunque considerásemos el modelo de esferas rígidas el
comportamiento cuántico seria diferente, disminuyendo las crestas y
elevándose los valles cerca de la barrera de potencial aparte del efecto
túnel en esta barrera.
Así pues en este capitulo trataremos de
la explicación del Método monte Carlo a líquidos con
comportamiento cuántico.
Aunque prescindiendo por supuesto de spin y
también de efecto de canje ( importante para el caso del Helio).
Ventajas de ``Metrópolis'' frente a ``crudo''.
Las ventajas de
aquel son que se evitan situaciones meta-estables (o
cuasi-ergodicas).
Representación en el lenguaje path-integral de las
partículas de un fluido (sin canje cuántico)
En el método
path- integral consiste en derivar la función densidad en función de
beta, surgiendo una función isomorfa de la función de
distribución con lo cual vamos a poder aplicar el mismo sistema que hemos
utilizado para el sistema clásico.
Va a implicar que cada
partícula se convierte en una cadena de seudo-partículas.
A
través de una intrincada deducción matemática vamos a llegar a
una importante ecuación que corresponde al diámetro de las cadenas.
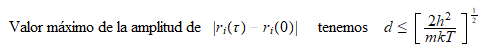 que es muy similar a la formula de De Broglie.
que es muy similar a la formula de De Broglie.
En el lenguaje
path-integral las partículas de un fluido sin canje cuántico se
representan por una cadena de eslabones de seudo partículas.
El
tratamiento Monte Carlo requerirá ahora tres parámetros delta que
regularemos para que el
n de intersecciones sea la, mitad que el de ensayos, ypsilon no correspondiendo
ahora a la posición de las partículas sino al centro de gravedad de
la cadena (tomando también aleatoriamente) y n o paso.
de intersecciones sea la, mitad que el de ensayos, ypsilon no correspondiendo
ahora a la posición de las partículas sino al centro de gravedad de
la cadena (tomando también aleatoriamente) y n o paso.
.
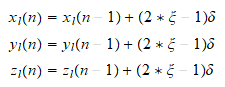
Temas 11 y 12
Modelo de red y estudio de las disoluciones, haciendo
especial hincapié en aspectos de índole técnico.
Alumno:
Francisco Cabot Pol \nobreakspace
\nobreakspace
DNI 22505880
n matricula 09-96-00766
matricula 09-96-00766
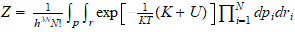
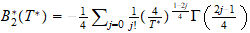
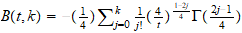
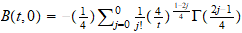
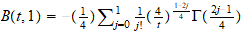
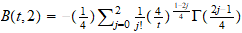
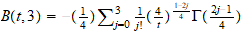
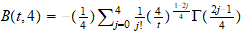
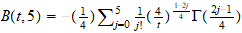
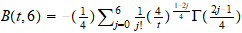
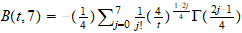
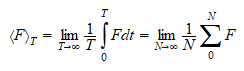 Demostraremos
que de todas las distribuciones posibles solo una, la máxima (que nos
permitirá aplicar la condición de máximo) contribuye
apreciablemente en el calculo de propiedades macroscópicas. De ese modo,
se van a determinar los números de ocupación (los cuales definen la
distribución) y, consiguientemente, la probabilidad de que un sistema
posea un valor de la energía y de los parámetros-y, a través de
la condición de máximo (aplicando la técnica de los
multiplicadores de Lagrange y utilizando la aproximación de Stirling).
Demostraremos
que de todas las distribuciones posibles solo una, la máxima (que nos
permitirá aplicar la condición de máximo) contribuye
apreciablemente en el calculo de propiedades macroscópicas. De ese modo,
se van a determinar los números de ocupación (los cuales definen la
distribución) y, consiguientemente, la probabilidad de que un sistema
posea un valor de la energía y de los parámetros-y, a través de
la condición de máximo (aplicando la técnica de los
multiplicadores de Lagrange y utilizando la aproximación de Stirling).