SISTEMA RECIPROCO
(trilogia)
Solo espacio&tiempo (1,2,3)
http://www.reciprocalsystem.com/bpm/
1.-NOMENCLATURE
2.- UNIDADES
3.- ISOTOPOS
4.- RADIOACTIVIDAD
5.- ESPECTRO ELECTROMAGNETICO
6.- EVALUACION TEORICA DE LA CONSTANTE DE PLANK
7.- LIMITE TERMICO
8.- RADIACION DE FONDO COSMICO
9- MECANICA CUANTICA
1.-NOMENCLATURE
http://reciprocal.systems/research/dof/ScalarSwitch.html
A) Basic speed / energy nomenclature and etheric levels:
| Energy | Right | Top | Back |
| 2 Counterspace(YIN) | 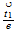 |
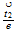 |
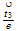 |
| 0 Border e-t | e,t | e,t | e,t |
| 1 Espace (YANG) | 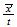 |
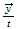 |
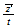 |
| Speed | Left | Bottom | Front |
27 Combinations:1 point, 6 line,12 plane, 8 volume
| 0 | 000 | 000...punto | nivel 4 |
| 1 | 001 | 00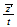 ...line ...line |
nivel 5 |
| 2 | 002 | 00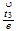 ...line ...line |
nivel 3 |
| 3 | 010 | 0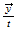 0...line 0...line |
nivel 5 |
| 4 | 011 | 0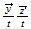 ...plane ...plane |
nivel 6 |
| 5 | 012 | 0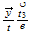 ...plane ...plane |
nivel 6 y 5 |
| 6 | 010 | 0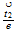 0...line 0...line |
nivel 5 |
| 7 | 021 | 0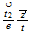 ...plane ...plane |
nivel 5 y 4 |
| 8 | 022 | 0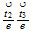 ...plane ...plane |
nivel 2 |
| 9 | 100 | 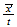 00...line 00...line |
nivel 5 |
| 10 | 101 | 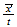 0 0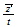 ...plane ...plane |
nivel 6 |
| 11 | 102 | 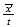 0 0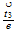 ...plane ...plane |
nivel 5 y 3 |
| 12 | 110 | 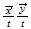 0...plane 0...plane |
nivel 6 |
| 13 | 111 | 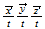 ...volume ...volume |
nivel 7 |
| 14 | 112 | 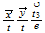 ...volume ...volume |
nivel 6 y 3 |
| 15 | 120 | 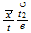 0...plane 0...plane |
nivel 5 y 3 |
| 16 | 121 | 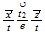 ...volume ...volume |
nivel 6 y 4 |
| 17 | 122 | 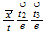 ...volume ...volume |
nivel 5 y 2 |
| 18 | 200 | 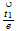 00...line 00...line |
nivel 3 |
| 19 | 201 | 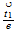 0 0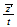 ...plane ...plane |
nivel 4 y 5 |
| 20 | 202 | 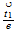 0 0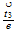 ...plane ...plane |
nivel 2 |
| 21 | 210 | 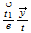 0...plane 0...plane |
nivel 3 y 5 |
| 22 | 211 | 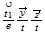 ...volume ...volume |
nivel 3 y 6 |
| 23 | 212 | 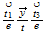 ...volume ...volume |
nivel 2 y 5 |
| 24 | 220 | 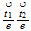 0...plane 0...plane |
nivel 2 |
| 25 | 221 | 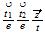 ...volume ...volume |
nivel 2 y 5 |
| 26 | 222 | 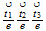 ...volume ...volume |
nivel 1 |
Counterspace(YIN)
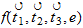
Espace (YANG)
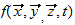
| 1 Counterspace(YIN) |
|
|||
3 Border
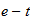 |
4
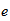 space scalar-
space scalar-
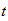 time scalar
time scalar |
|||
| 2 Espace (YANG) |
|
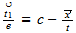
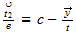
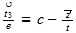
--------------------------------------------
B) Extended Nomenclature:
∠s 2220 single rotation, electric
angle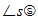
∢s 2222 double rotation, solid/magnetic
angle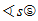
t 23f0 clock time t
⭙s 2b59 equivalent
space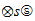
∿s 223f birotation (Re, Im
axis)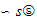
2100a ℊ ℜ 210a, 211c
real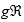
ℑ 2111
imaginary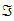
ℂ 2102
complex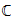
ℝ 211d real
numbers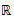
ℕ 2115 natural
(1+)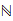
ℤ 2124
integers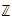
ℚ 211a
rational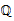
ℋ 210b quaternion
ℎ 210e planck
constant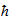
ℏ 201f reduced
planck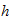
℃ 2103
Centigrade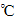
℉ 2109
Fahrenheit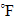
Ω 2126
Resistance,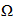
ohms ℧ 2127 Conductance,
siemens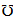
2.- UNIDADES
La
energia natural o unitaria es la energia del atomo de hidrogeno = 1 Hartree
(dos veces la energia de ionizacion del hidrogeno)
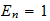 Hartree
energy=
Hartree
energy=
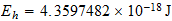
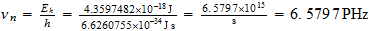
Espacio unitario en el sistema unitario
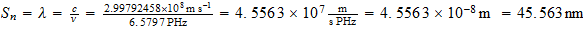
Tiempo
unitario en el Sistema Reciproco
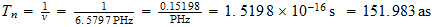
Velocidad unitaria en el sistema reciproco
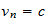
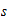 |
space | 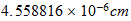 |
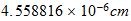 |
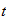 |
time | 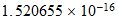 |
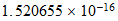 |
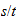 |
speed | 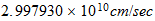 |
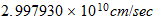 |
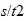 |
acceleration | 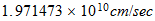 |
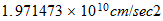 |
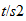 |
force | 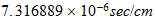 |
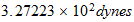 |
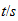 |
energy | 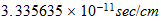 |
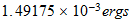 |
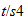 |
pressure | 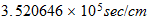 |
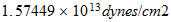 |
 |
momentum | 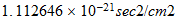 |
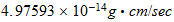 |
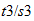 |
inertial mass | 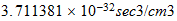 |
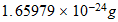 |
| Unidades Espacio-tiempo | Unidades Convencionales |
http://reciprocal.systems/research/units.php
3.- ISOTOPOS
http://www.reciprocalsystem.com/bpm/bpm24.htm
Niveles de ionzación
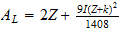
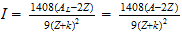
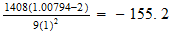
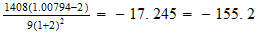
http://www.reciprocalsystem.com/bpm/bpm24.htm
http://www.reciprocalsystem.com/ce/iratio.htm
Masa vibratoria=nivel de
ionizacion
magnetica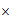 masa
rotacional
masa
rotacional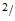 relacion
interregional
relacion
interregional
Peso
atomico=
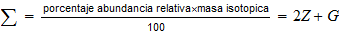
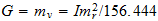
interregional ratio
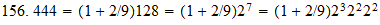
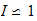
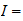 nivel de ionización magnetica
nivel de ionización magnetica
Peso
atomico=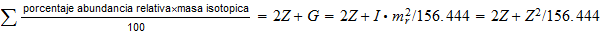
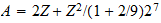
| Numero atomico |
Numeros magicos
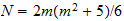
| numeros naturales |
m=1,2,3,4,5,6,7,8...
Nuevo numero magico Calcio 52
http://hyperphysics.phy-astr.gsu.edu/hbasees/nuclear/shell.html
http://www.agenciasinc.es/Noticias/Un-experimento-del-CERN-revela-un-nuevo-numero-magico-en-un-nucleo-atomico
http://hyperphysics.phy-astr.gsu.edu/hbasees/nuclear/shell.html#c2
http://milan.milanovic.org/math/english/atom/proton.html
http://milan.milanovic.org/math/english/atom/proton.html
Sistema
hererado
http://cienciaxxi.es/blog/?p=5878
4.-
RADIOACTIVIDAD
http://www.reciprocalsystem.com/bpm/bpm25.htm
5.- ESPECTRO ELECTROMAGNETICO
Cada dimensión escalar puede ser desplazado una sola unidad hacia la velocidad (s / t) o energía (t / s), desde el punto de la unidad (velocidad de la luz) neutral. Larson se refiere a estos como los primeros y segundos unidades de movimiento (que en realidad son Desplazamientos ), por lo que tiene la apariencia de que tres, dimensiones escalares tienen un total de seis "unidades de movimiento."
Cuando estas unidades se aplican dimensionalmente, que tiene un máximo de 2 3 = 8 posibilidades, no seis. Los estudiantes normalmente se piensa en esto como "2 direcciones, 3 dimensiones", por lo que tiene un 2x2x2 "cubo" de movimiento. Pero no es un cubo, es sólo los posibles grados de libertad. Además, el punto de unidad neutral también debe ser considerado, por lo que no son técnicamente 3 3 = 27 posibles grados de libertad, que incluyen cero, 1D y 2D desplazamientos.
Haga clic en el ratón por encima, por debajo o en los interruptores para cambiar las diversas posibilidades. La imagen de "geometría de coordenadas" es sólo para ayudar en la visualización mediante la asignación de los tres, dimensiones escalares a los ejes de coordenadas. En la "vida real", que no hace eso y se acaba la imagen "Movimiento neto", donde se superponen las dimensiones (una línea es una línea, no importa en qué dirección se señala) con. He seleccionado arbitrariamente el eje X para representar todo el movimiento lineal y el plano XY para representar todo movimiento planar (2D).
Texto copiado
Golden Ratio
Quote
Post by bperet » Mon Jan 23, 2017 2:22 pm
This is from a private email between Gopi and myself:
I was working on how speed in the space region would relate to speed in the time region, trying to see what positron flow through the space region would look like, and came up with something interesting...
From the material sector...
The space region is electric, 1-dimensional speed, v1.
The time region is magnetic, 2-dimensional "orbital velocity", v2
Since we measure in the 1-x range, as "x", we do not account for the unit speed boundary between them, so we would see that unit speed IN ADDITION to whatever electric velocity was on the other side (why cosmic is faster than light). This gives the relationship:
v2 (TR) = 1 (unit speed) + v1 (SR)
Unless I did the math wrong, v is a constant ratio:
v = +1.618... or -0.618...
Which appears to be the Phi, the Golden Ratio. This tells me that in life, where you have substantial TR/SR ratios, the point of rotational stability would not be at unity--but at the Golden Ratio, simply because of the way our senses work in the Material sector (x -> 1, rather than 1 -> x).
------------------------------------------------------------------
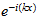
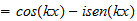
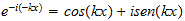
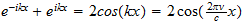
--------------------------------------------------------------------
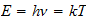
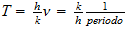
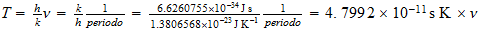
 |
 |
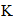 |
Hartees | |
| Ionizantes | 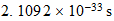 |
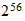 |
||
| Ionizantes | ||||
| Ionizantes | ||||
| No ionizante/Ionizante | 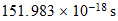 |
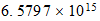
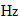 |
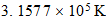 |
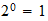 |
| No ionizantes | ||||
| No ionizantes | ||||
| No ionizantes | 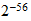 |
contraespacioespacio rotacional
e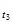 |
|
|||||||||||||||||
espacio
e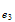 |
|
| Periodo minimo | Hartrees | |
| Sistema heredado-Tiempo de Plank | 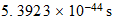 |
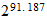 |
| Sistema reciproco | 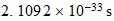 |
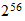 |
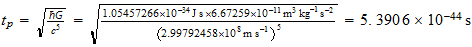
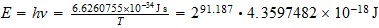 ,
Solution is:
,
Solution is:
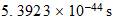
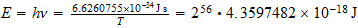 ,
Solutionis
,
Solutionis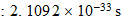
6.- EVALUACION TEORICA DE LA CONSTANTE DE PLANK
Evaluación Teórica de la constante de Planck
Prof. KVK Nehru, Ph.D.
El análisis de las cantidades físicas en sus componentes de espacio-tiempo, posible gracias a la aplicación del Sistema Recíproca, arroja nueva iluminación de la naturaleza y el significado de estas cantidades. Larson demuestra que el resultado de aplicar el postulado de unidad discreta a las dimensiones de física cantidades resultados en el principio de que las dimensiones del numerador de la expresión espacio-tiempo de cualquier cantidad física real no puede ser mayor que las del denominador. Citando Larson: 1
El más notable de las cantidades excluidas por este principio dimensional
es ''acción''. Este es el producto de la energía,
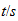 ,
y el tiempo
,
y el tiempo
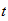 ,
y en términos de espacio-tiempo es
,
y en términos de espacio-tiempo es
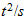 Por lo tanto, no es admisible como una cantidad física de bienes ... La
ecuación de la conexión de la energía de la radiación con
la frecuencia es:
Por lo tanto, no es admisible como una cantidad física de bienes ... La
ecuación de la conexión de la energía de la radiación con
la frecuencia es:
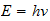
donde
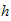 es la constante de Planck ... se expresa en términos de acción. Es
claro, sin embargo, a partir de la explicación de la naturaleza de los
fotones de la radiación ... que el denominada ''frecuencia'' es en
realidad una velocidad. Se puede expresar como una frecuencia sólo porque
el espacio que está implicado es siempre una magnitud unidad. En
realidad, la dimensión espacial pertenece con la frecuencia, no con la
constante de Planck. Cuando se transfiere así, ... la ecuación de la
energía de la radiación es [en términos de espacio-tiempo]
es la constante de Planck ... se expresa en términos de acción. Es
claro, sin embargo, a partir de la explicación de la naturaleza de los
fotones de la radiación ... que el denominada ''frecuencia'' es en
realidad una velocidad. Se puede expresar como una frecuencia sólo porque
el espacio que está implicado es siempre una magnitud unidad. En
realidad, la dimensión espacial pertenece con la frecuencia, no con la
constante de Planck. Cuando se transfiere así, ... la ecuación de la
energía de la radiación es [en términos de espacio-tiempo]
 (1)
(1)
En la estructura del Universo Físico Larson deriva el valor de la constante de Planck sobre esta base, haciendo uso de la constante de gravitación. En este trabajo trato de hacer lo mismo, pero sin llevar la constante de gravitación en la imagen, con la esperanza de mostrar los factores que intervienen con mayor claridad. Adoptaremos el sufijo c para indicar una cantidad expresada en unidades convencionales, sin sufijo para indicar el cantidad expresada en las unidades naturales, y el sufijo n para indicar la magnitud de la unidad natural de un cantidad expresada en términos de unidades convencionales. Recordando que, sobre la base unidad natural, cualquier unidad de una cantidad física es también la unidad de la correspondiente cantidad inversa; cada unidad de energía es tanto una unidad de t / s y una unidad de s / t, cada uno en su contexto adecuado. 2 De la ecuación ( 1), la relación cuantitativa entre E unidades naturales de energía y u unidades naturales de la velocidad se puede expresar como: E = (1/1) u ya que la magnitud numérica de la t 2 / S 2 término es (1/1) 2 en unidades naturales. La velocidad u está dado por la cociente de S unidades naturales de espacio y de T unidades naturales de tiempo. Por lo tanto, E = S / T 1 Larson, Dewey B., Nada más que de movimiento , Editores del Pacífico Norte: Portland, OR, 1979, p. 152 . 2 Ibid., p. 169 (véanse las líneas 6-4 de la parte inferior). Reciprocidad 12 ? 3 página 6 Copyright © 1983 por ISUS, Inc. Todos los derechos reservados. Rev. 7
Página 2
2 Evaluación Teórica de la constante de Planck Ahora vamos a introducir las unidades convencionales en la ecuación, pero haremos lo que sólo en el caso de los cantidades que queremos que expresan en las unidades convencionales finalmente. Puesto que E = E c / E n y T = T c / T n , tenemos: E c = (E n T n ) S T c (2) Sin embargo, a partir de lo que se ha citado anteriormente, se observa que la magnitud numérica S en la ecuación ( 2) es 1, ya que la vibración se limita a una unidad natural de espacio. La falta de reconocimiento de la condición verdadera del término frecuencia como término velocidad y expresar todas las cantidades en unidades convencionales (es decir, incluyendo 1 cm en lugar de la S), por tanto, tiene el efecto de exagerar el valor numérico a la derecha- lado por un factor de 1 cm / S n . Como tal, el lado derecho se debe multiplicar por el recíproco de este factor. Por lo tanto, E c (En ergios) = ( E n T n S n 1 cm ) 1 T c (En segundos) (3) O, en sustitución de 1 / T por v, la frecuencia en hercios, E C = ( E n T n S n 1 cm ) v (4) de la que tenemos la constante de Planck como: H = E n T n S n 1 cm (5) Hay dos factores adicionales a tener en cuenta antes de que podamos llegar a la magnitud numérica de h. En primer lugar, ya que la vibración de fotones se limita a la región de tiempo mientras que las mediciones Pertenecen a la fuera de la región, este valor de h es para ser reducida por la relación R. interregional Por lo tanto, h = ( E n T n S n ) ( R \ 1 cm ) (6) El segundo factor es que se trate con el efecto de la componente de masa s secundaria. Mientras la masa es expresado en la unidad dinámica de gramo, se hace necesario tener en cuenta la discrepancia entre las unidades de masa primaria y la masa inercial. Por lo tanto, al adoptar la gram-unidad, el término de masa es que ser multiplicado por un factor de 1 + s, donde 1 es la masa primaria y s la masa secundaria. 3 En el presente caso, ya que la energía es t / s, mientras que la masa es t 3 / S 3 , El factor multiplicador es (1 + s) Tercera . Por lo tanto, h = [ ( E n T n S n ) ( R \ 1 cm ) ] [1 + s] Tercera (7) 3 Ibid., p. 170 .
Página 3
Evaluación Teórica de la constante de Planck 3 La adopción de
los valores de la nada sino de movimiento 4, 5,6 , E n = 1,49175 \ 10 -3 ergio
T n = 1.520655 \ 10 -16 segundo S n = 4.558816 \ 10 -6 cm R n = 156.4444
(Referencia 5) , y para el cálculo de la masa secundaria, a partir de
Referencia 6, m, la masa magnética = 0.00639205, tenemos el valor de la
constante de Planck como: h = 6.6243162 \ 10 -27 erg-sec (8) Pero hay que
señalar que m, la masa magnética, no es el único componente de
la s masa secundaria. Esto es porque en las partículas con desplazamiento
neto de la unidad (como, por ejemplo, M
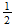 -
-
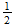 -0), siempre hay una unidad inicial de la masa eléctrica, de magnitud
0,0005787. Por lo tanto 1 + s se convierte en 1,00697075. Sustituyendo esto en
la ecuación (7) da: h = 6.6255857 \ 10 -27 erg-sec (9) Esto es en
estrecho acuerdo con el valor experimental de 6,6256 \ 10 -27 erg-segundos
(con un error de 2,16 \ 10 -4 por ciento)
-0), siempre hay una unidad inicial de la masa eléctrica, de magnitud
0,0005787. Por lo tanto 1 + s se convierte en 1,00697075. Sustituyendo esto en
la ecuación (7) da: h = 6.6255857 \ 10 -27 erg-sec (9) Esto es en
estrecho acuerdo con el valor experimental de 6,6256 \ 10 -27 erg-segundos
(con un error de 2,16 \ 10 -4 por ciento)
http://www.reciprocalsystem.com/rs/cwkvk/planck.htm
E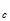 =
h
=
h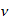
En nuestro sistema reciproco de espacio-tiempo:
E=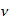
es decir
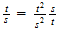
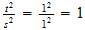
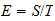
siendo
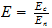
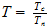
de donde:
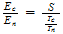
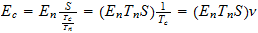
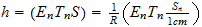
Precisando:
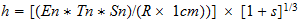
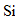 endo:
endo:
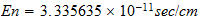 equivalente a
equivalente a
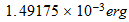 puesto en ergios
puesto en ergios
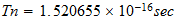
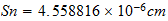
En = Natural unit of Energy
Tn = Natural unit of Time
Sn = Natural unit of Space
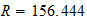
Atomic rotation:
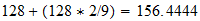
Subatomic rotation:
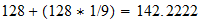
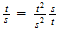
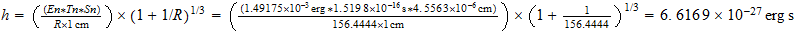
= 6.6255857\10-27 erg-sec
Current value of h = 6.6256\10-27erg-sec [within 2\ 10-4 %]
Unit space (s): 4.5563352671 x 10-6 cm
Unit time (t) : 1.5198298508 x 10-16 s
Unit speed (s/t): 299,792,458 m/s (exact)
Inter-regional Ratio (R):
--------------------------------------------------------------------------------------
Constante de Plank como función del Numero de Avogadro
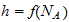 :
:
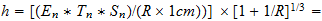
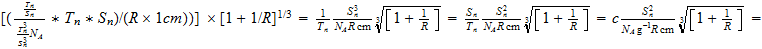
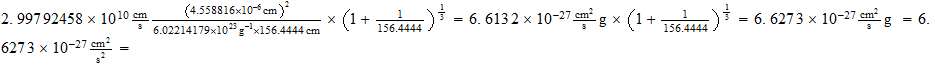
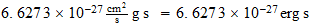
Constante de Plank como función del Numero de Avogadro
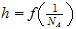 :
:
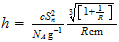
7.- LIMITE TERMICO
En el caso de la derivacion de la constante de Plank, si que veo correcta la
utilizacion de
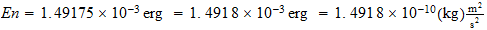
Equivalente a la masa atomica unitaria
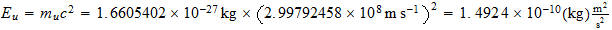
Pero para en la deduccion del limite termico no se debe utilizar
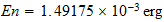 como hace Larson y se debe utilizar como energia natural unitaria el valor de
1Hartree.
como hace Larson y se debe utilizar como energia natural unitaria el valor de
1Hartree.
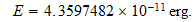
Que por una simple proporcionalidad con la temperatura de fondo cosmico
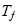 nos conduce a la temperatura de explosion de la supernovas
nos conduce a la temperatura de explosion de la supernovas
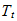 cuando
alcanzan el nucleo de hierro-niquel en el contraespacio.
cuando
alcanzan el nucleo de hierro-niquel en el contraespacio.
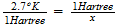
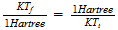
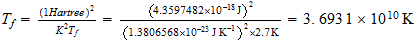
36 mil millones de grados, bastante de acuerdo con la literatura cientifica
y tres ordenes inferior al resultado de Prof. K.V.K. Nehru, Ph.D. en su trabajo:
Intrinsic Variables, Supernovae and the Thermal Limit
Prof. K.V.K. Nehru, Ph.D.
Que obtine una temperatura de explosion del orden de
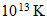
http://reciprocalsystem.org/PDFa/Intrinsic%20Variables,%20Supernovae%20and%20the%20Thermal%20Limit%20(KVK,%20Nehru).pdf
Ya que utiliza
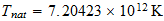
Es decir una
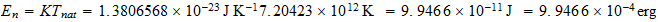
Bibliografia:.
http://www.astroscu.unam.mx/~wlee/OC/SSAAE/AAE/Supernovas/Explosion%20de%20supernova.html
http://www.scienceinschool.org/print/528
....Cuando este material nuclear se agota la temperatura y presión de la estrella
aumenta de forma notable hasta que comienza a formar ...En ese momento su
temperatura nuclear puede ser de 70 mil millones de grados y cuando agota el
Hierro la estrella se vuelve inestable y ... El fenómeno de la explosión de una
supernova es similar al de la explosión de una Nova, pero con la diferencia
sustancial de ...
http://books.google.es/books?id=Klc_JmXMF_8C&pg=PT18&lpg=PT18&dq=temperatura+en+las+explosiones+termonucleares+de+las+supernovas+millones+de+grados&source=bl&ots=I-nspfHNXs&sig=VF4OH203XTaSjaRH0U5yA18mOyI&hl=es&sa=X&ei=2FP3Upn0Js3M0AW_IA&ved=0CEwQ6AEwBQ#v=onepage&q=temperatura%20en%20las%20explosiones%20termonucleares%20de%20las%20supernovas%20millones%20de%20grados&f=false
books.google.es/books?isbn=8468609544
-------------------------------------------------------------------------------------------------------
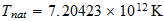
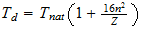
En el intervalo de
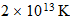 a
a
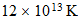 estaria dentro de la gama de energias de los rayos cosmicos, lo cual
representaria las temperaturas que se alcanzan en las explosiones de las
supernovas
estaria dentro de la gama de energias de los rayos cosmicos, lo cual
representaria las temperaturas que se alcanzan en las explosiones de las
supernovas
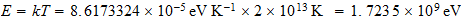
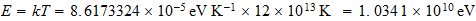
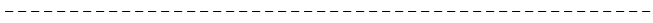
This
range would be within the range of energies of cosmic rays, which would
represent the temperatures reached in supernova explosions;
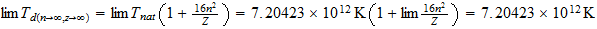
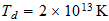
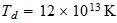
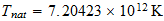
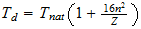
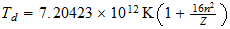
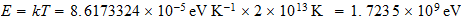
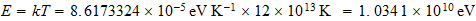
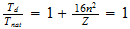
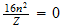

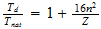
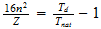
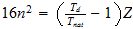
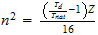
n=max ((a-1), b)
Displacement Element Atomic No.
2-1-0 He 2
2-2-0 Ne 10
3-2-0 Ar 18
3-3-0 Kr 36
4-3-0 Xe 54
4-4-0 Rn 86
masa magnetica
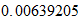
masa electrica
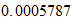
1+s=1+R=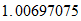
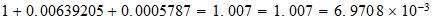
Elemento a-b-c
Serie b=1
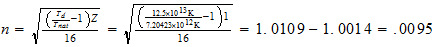 H
M l-l-(l) a-1=0
H
M l-l-(l) a-1=0
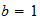 resultado
resultado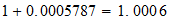
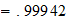
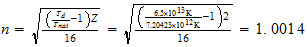 He
2-1-0
He
2-1-0 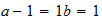 resultado
resultado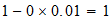
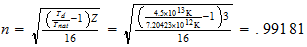 Li
2-1-1
Li
2-1-1
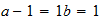 resultado
resultado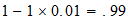
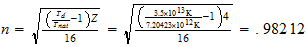 Be
2-1-2
Be
2-1-2 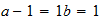 resultado
resultado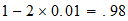
 B
2-1-3
B
2-1-3 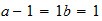 resultado
resultado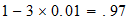
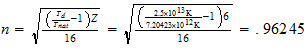 C
2-1-4
C
2-1-4
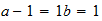 resultado
resultado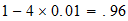
0
2-2--(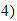
Serie b=2a
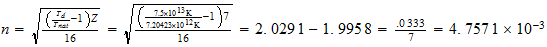 N
2-2-(3)
N
2-2-(3) 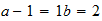 resultado
resultado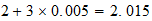
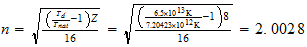 O
2-2-(2)
O
2-2-(2) 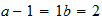 resultado
resultado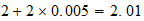
 F
2-2-(l)
F
2-2-(l)
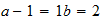 resultado
resultado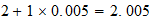
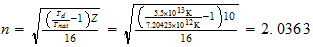 Ne
2-2-0
Ne
2-2-0
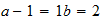 resultado
resultado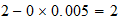
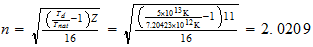 Na
2-2-1
Na
2-2-1
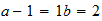 resultado
resultado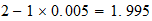
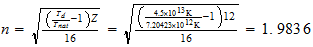 Mg
2-2-2
Mg
2-2-2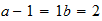 resultado
resultado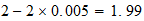
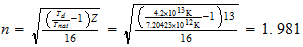 Al
2-2-3
Al
2-2-3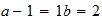 resultado
resultado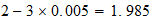
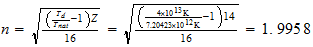 Si
2-2-4
Si
2-2-4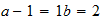 resultado
resultado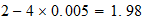
Serie b=2b
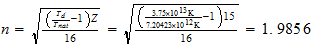 P
3-2-(3)
P
3-2-(3)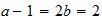 resultado
resultado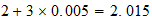
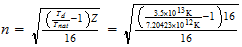
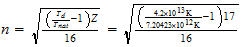
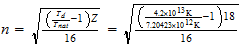
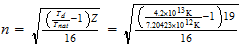
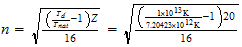
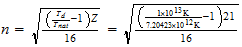
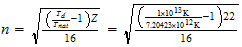
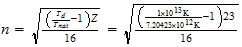
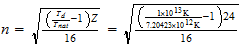
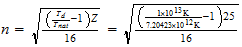
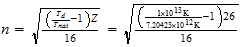
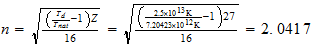 Co
3-2-9
Co
3-2-9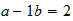 resultado
resultado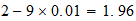
Serie b=3
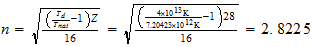 Ni
3-3-(8)
Ni
3-3-(8)
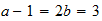 resultado
resultado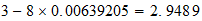
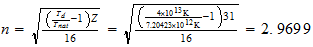 Ga
3-3-(5)
Ga
3-3-(5)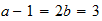 resultado
resultado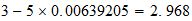
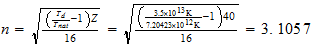 Zr
3-3-4
Zr
3-3-4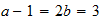 resultado
resultado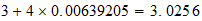
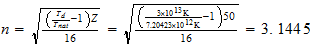 Sn
4-3-(4)
Sn
4-3-(4)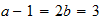 resultado
resultado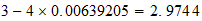
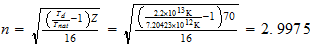 Yb
4-3-16
Yb
4-3-16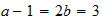 resultado
resultado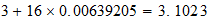
Serie b=4
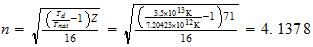 Lu
4-4-(15)
Lu
4-4-(15)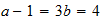 resultado
resultado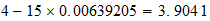
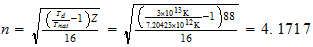 Ra
4-4-2
Ra
4-4-2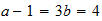 resultado
resultado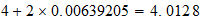
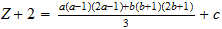
C 2-1-4
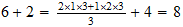
Element Displacement c/vm c/ve Trans. Eff. Calculated Observed
H M l-l-(l)
M
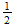 -
-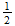 -(1)
v6 1/2 * 2 13.585 13.598
-(1)
v6 1/2 * 2 13.585 13.598
He 2-1-0 17¶¶ 1/2.5 * 1/1.5 24.95 24.587
Li 2-1-1 2 1/3 * 1/2 5.55 5.392
Be 2-1-2 3 1/2 * 1/3 9.61 9.322
B 2-1-3 3 1/2 * 1/4 8.94 8.298
C 2-1-4 5 1/3 * 1/2 11.09 11.260
N 2-2-(3) 14¶¶ 1/3 * 1/3 18.07
6¶¶ 1/3 * 1/3 11.21
Av. 14.64 14.534
O 2-2-(2) 15¶¶ 1/3 * 1/3 18.75
7¶ 1/3 * 1/3 12.28
Av. 15.51 13.618
F 2-2-(l) 16¶¶ 1/3 * 1/2.5 20.31
8¶ 1/2.5 * 1/2.5 14.52
Av. 17.42 17.422
Ne 2-2-0 17¶¶ 1/2.5 * 1/2.5 21.96 21.564
Na 2-2-1 2 1/3 * 1/2.5 5.25 5.139
Mg 2-2-2 3 1/2.5 * 1/2.5 7.76 7.646
Al 2-2-3 3 1/3 * 1/4 8.08 5.986
Si 2-2-4 3 1/2.5 * 1/4.5 8.21 8.151
P 3-2-(3) 6¶ 1/4 * 1/3 10.43 10.486
S 3-2-(2) 7¶ 1/2.5 * 1/4 11.96
4 1/2.5 * 1/7¶ 8.49
Av. 10.22 10.360
Cl 3-2-(l) 8¶ 1/2.5 * 1/4 12.91 12.967
Ar 3-2-0 17¶¶ 1/4 * 1/3 18.65
13.19
15.92 15.759
K 3-2-1 2 1/4 * 1/3 4.66 4.341
Ca 3-2-2 3 1/4 * 1/3 6.60 6.113
Sc 3-2-3 3 1/4 * 1/4 7.52 6.54
Ti 3-2-4 3 1/4 * 1/5 7.11 6.82
V 3-2-5 3 1/4 * 1/6 6.79 6.74
Cr 3-2-6 3 1/3.5 * 1/7 6.76 6.766
Mn 3-2-7 4 1/3 * 1/8 7.84 7.435
Fe 3-2-8 4 1/2.5 * 1/9 7.97 7.870
Co 3-2-9 4 1/2.5 * 1/9.5 7.86 7.86
Ni 3-3-(8) 4 1/2.5 * 1/10.5+ 7.67 7.635
Cu 3-3-(7) 4 1/2.5 * 1/7.5§ 7.67 7.726
Zn 3-3-(6) 4 1/4 * 1/3¶ 9.33 9.394
Ga 3-3-(5) 4¶ 1/4 * 1/4 7.52 5.999
Ge 3-3-(4) 4 1/4 * 1/51 . 8.21 7.899Electric Ionization 9
Specific Speed EI in eV
Element Displacement c/vm c/ve Trans. Eff. Calculated Observed
As 3-3-(3) 6¶ 1/4 * 1/4 9.70 9.81
Se 3-3-(2) 7¶ 1/3.5 * 1/3.5 11.36
4 1/3.5 * 1/6.5¶ 7.95
Av. 9.66 9.752
Br 3-3-(l) 8¶ 1/4 * 1/3.5 11.87 11.814
Kr 3-3-0 9¶ 1/3.5 * 1/3.5 13.12 13.999
Rb 3-3-1 2 1/4 * 1/4 4.34 4.177
Sr 3-3-2 3 1/4 * 1/4 6.14 5.695
Y 3-3-3 4 1/4 * 1/4 7.52 6.38
Zr 3-3-4 4 1/4 * 1/5 8.21 6.84
Nb 3-3-5 4 1/4 * 1/6 7.84 6.88
Mo 3-3-6 4 1/4 * 1/7 7.55 7.099
Tc 3-3-7 4 1/4 * 1/8 7.30 7.28
Ru 3-3-8 4 1/3.5 * 1/8.5 7.43 7.37
Rh 3-3-9 4 1/3.5 * 1/9.5 7.23 7.46
Pd 4-3-(8) 5 1/3.5 * l/8.5§ 8.31 8.34
Ag 4-3-(7) 4 1/4.5 * 1/7.5§ 7.20 7.576
Cd 4-3-(6) 4 1/5 * 1/3¶ 8.82 8.993
In 4-3-(5) 4¶ 1/5 * 1/4 7.11 5.786
Sn 4-3-(4) 4 1/5 * 1/5¶ 7.76 7.344
Sb 4-3-(3) 5 1/4 * 1/6¶ 8.77 8.641
Te 4-3-(2) 5 1/3.5 * 1/6.5¶ 8.89 9.009
I 4-3-(l) 8¶ 1/5 * 1/4 10.86 10.451
Xe 4-3-0 9¶ 1/4.5 * 1/3.5 12.32 12.130
Cs 4-3-1 2 1/5 * 1/4 4.12 3.894
Ba 4-3-2 3 1/5 * 1/4 5.80 5.212
La 4-3-3 4 1/5 * 1/4 7.11 5.577
Dy 4-3-12 4 1/5 * 1/13 6.11 5.93
Ho 4-3-13 4 1/5 * 1/14 6.00 6.02
Er 4-3-14 4 1/5 * 1/15 5.90 6.10
Tm 4-3-15 4 1/4.5 * 1/15.5 6.01 6.18
Yb 4-3-16 4 1/4.5 * 1/16.5 5.91 6.254
Lu 4-4-(15) 4+ 1/5 * 1/18+ 5.64 5.426
Hf 4-4-(14) 5 1/4.5 * 1/14.5§ 6.83 7.0
Ta 4-4-(13) 4¶¶ 1/4.5 * 1/4.5 7.09 7.89
W 4-4-(12) 5¶¶ 1/5 * 1/4.5 7.97 7.98
Re 4-4-(ll) 5 1/5 * 1/6¶¶ 8.29 7.88
Os 4-4-(10) 7¶¶ 1/5 * 1/5 9.51
5 1/5 * 1/7¶¶ 7.98
Av. 8.74 8.7
Ir 4-4-(9) 8¶¶ 1/5 * 1/5 10.27
5 1/4.5 * 1/7.5¶¶ 8.05
Av. 9.16 9.1
Pt 4-4-(8) 1/5 * 1/5 10.9810 Electric Ionization
Specific Speed EI in eV
Element Displacement c/vm c/ve Trans. Eff. Calculated Observed
5 1/5 * 1/9¶¶ 7.49
Av. 9.23 9.0
Au 4-4-(7) 5 1/5 * 1/8 § 7.72
5 1/5 * 1/2¶ 10.91
Av. 9.31 9.225
Hg 4-4-(6) 5 1/4.5 * 1/2.5¶ 10.60 10.437
T1 4-4-(5) 4¶ 1/5 * 1/5 6.72 6.108
Pb 4-4-(4) 5¶ 1/5 * 1/5 7.76 7.416
Bi 4-4-(3) 5 1/5 * 1/6¶ 8.29 7.289
Po 4-4-(2) 5 1/4.5 * 1/6.5¶ 8.35 8.42
Rn 4-4-0 9¶ 1/5 * 1/5 10.98 10.748
Ra 4-4-2 3 1/5 * 1/5 5.49 5.279
Ac 4-4-3 4 1/5 * 1/4.5 6.90 6.9
Th 4-4-4 5 1/5 * 1/5 1.16 6.95
Note:
+ Alternative all-positive displacement
§ Inverse electric speed (in transverse effect only)
¶ 8-unit zero-shift (in the electric dimension)
¶¶ 16-unit zero-shift
Intrinsic Variables, Supernovae and the Thermal Limit
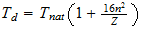
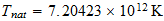
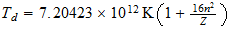
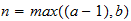
Element Displacement a-b-c
Serie b=1 H 1-1-(1) C 2-1-4
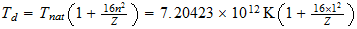
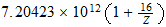

Serie b=2 N 2-2-(3) Co 3-2-9
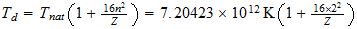
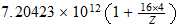
Serie b=3 Ni 3-3-(8)
 Yb
4-3-16
Yb
4-3-16
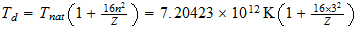
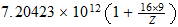

Serie b=4 Lu 4-4-(15) Ra 4-4-2
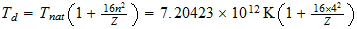
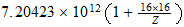
Thermal
Limit
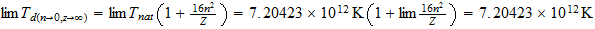
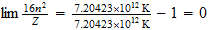
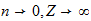
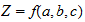
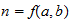
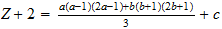
Thermal Limit
http://www.reciprocalsystem.com/bpm/bpm05.htm
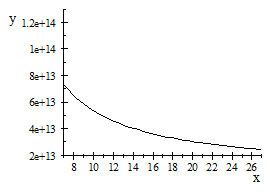
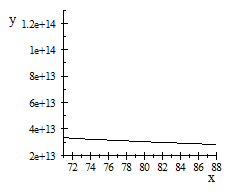
Dividing the gas constant by Avogadros number, 6.02486 x 1023 per g-mole, we obtain the Bolzman constant, the corresponding value on a single molecule basis: 1.38044 x 10-16 ergs/deg. As indicated earlier, this is two-thirds of the natural unit, and the natural unit of specific heat is therefore 2.07066 x 10-16 ergs/deg. We then divide unit energy, 1.49175 x 10-3 ergs, by this unit of specific heat, which gives us 7.20423 x 1012 degrees Kelvin, the natural unit of temperature in the region outside unit distance (that is, for the gaseous state of matter).
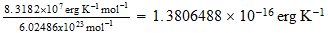
R=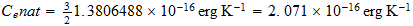
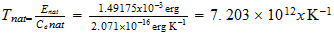
También vamos a estar interesado en la temperatura de la unidad en la T 3 base, la temperatura a la que el movimiento térmico llega a la región el tiempo límite. La potencia de 3/4 de 7,20423 x 10 12 es 4,39735 x 10 9 . Pero el movimiento térmico es un movimiento de la materia e implica el 2.9 Además de vibración para el movimiento lineal distribuido rotación de los átomos. Esto reduce la unidad de temperatura efectiva por el factor 1 + 2/9, el resultado es 3,5978 x 10 9 grados K.
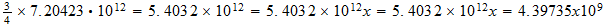 ????
????
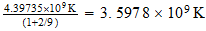
Todo el intervalo electromagnetico de
10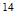
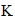 hasta
10
hasta
10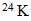 queda como una incognita?.
queda como una incognita?.
| Tipo de actividad | intervalo electromagnetico contraespacio | Accion en el espacio | intervaloelectromagnetico en el espacio |
| Actividad desconocida | 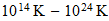 |
? | 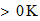 |
| Actividad nuclear (*) | 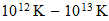 |
Cosmic Background Radiation | 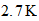 |
| Actividad bioquimica | 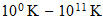 |
(*)Prof. K.V.K. Nehru, Ph.D.
Intrinsic Variables, S su upernovae and the Thermal Limit
http://rs2theory.org/node/11
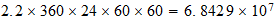
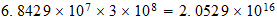
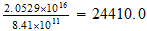
8.- RADIACION DE FONDO COSMICO
http://en.wikipedia.org/wiki/Cosmic_microwave_background
Radiación Cósmica de FondoRadiación Cósmica de Fondo: Origen y Temperatura Prof. KVK Nehru, Ph.D. 1 El Sector Cosmic Uno de los logros del sistema recíproco de la teoría es el descubrimiento del hecho que el universo físico no se limita a nuestro mundo familiar de tres dimensiones del espacio y uno dimensión del tiempo, el sector de material que Larson llama. En virtud de la simetría entre la naturaleza intrínseca del espacio y del tiempo, salen a la luz por Larson, demuestra la existencia de un sector cósmico del universo físico, en el que las relaciones espacio-temporales son inversa de los afín a la sector de material. Las características normales del sector cósmica podrían estar representados en un temporal de tres dimensiones fijas marco de referencia, al igual que los del sector material podría ser representado en una, de tres dimensiones fijas sistema de referencia espacial. En el universo de movimiento, el dato natural en el que el universo físico es incorporado es el movimiento hacia el exterior progressional de espacio-tiempo a la velocidad de la unidad (que se identifica como la velocidad de la luz). Las entidades del sector de material son el resultado del desplazamiento hacia abajo desde el Velocidad del fondo de la unidad (velocidades menores que la unidad), mientras que las del sector cósmica son el resultado de desplazamiento hacia arriba de la unidad (velocidades mayores que la unidad). Pero las entidades-como la radiación que se mueven a la velocidad de la unidad, siendo así en el límite entre los dos sectores, son fenómenos que son comunes a estos dos sectores. La gravitación, siendo siempre en oposición a la progresión espacio-tiempo hacia el exterior, hacia el interior es en escalar dirección en los marcos de referencia espaciales o temporales tridimensionales. Como el movimiento independiente en el sector de material (espacio tridimensional) es movimiento en el espacio, la gravitación en nuestro sector actúa hacia el interior en el espacio y los resultados de los agregados a gran escala de la materia. La gravitación del sector cósmico actúa aún hacia adentro pero es hacia el interior en el tiempo de tres dimensiones en lugar de en el espacio. En consecuencia, el sector de la cósmica equivalentes de las estrellas y las galaxias son agregados en tiempo y no en el espacio. Además, como Larson señala que ''... los diversos procesos físicos a los que la materia es objeto alterar posiciones en el espacio de forma independiente de las posiciones en el tiempo, y viceversa. Como resultado, los átomos de un agregado material, que son contiguas en el espacio, están muy dispersos en el tiempo, mientras que los átomos de un agregado cósmico, que son contiguos en el tiempo, están muy dispersos en el espacio ... ''Radiación se mueve a velocidad de la unidad con respecto a ambos tipos de sistemas de referencia fijos, y puede por lo tanto, ser detectados en ambos sectores, independientemente de dónde se origina. Así que recibimos la radiación de las estrellas y otros objetos cósmicos cósmicos tal como lo hacemos a partir del correspondiente agregados materiales. Pero estos objetos cósmicos no son agregados en el espacio. Ellos son distribuidos al azar en el sistema de referencia espacial. Por tanto, su radiación es recibido en el espacio a una intensidad baja y en una distribución isotrópica. Tal radiación de fondo es en realidad está recibiendo ''. 1 1 Dewey B. Larson, Los hechos Desatendidas de la Ciencia , Pub Pacífico Norte., Oregon, EE.UU., 1982, pp 72-73 . Reciprocidad 19 ? 4 página 20 Copyright © 2012 por ISUS, Inc. Todos los derechos reservados. Rev. 4
Página 2
2 Radiación Cósmica de Fondo 2 La temperatura de la radiación Una aproximación a la derivación de la temperatura de esta radiación cósmica de fondo se describe ahora. Esto se puede ver a implicar la consideración de varios otros artículos derivados anteriormente como la relativa abundancias cósmicas de los elementos y sus límites destructivos térmicos. En este sentido, por lo tanto, la El presente análisis tiene que ser tratado como provisionales-una revisión en la derivación de estos artículos haría implicar una modificación correspondiente en la presente derivación. A pesar de esto, el general enfoque de la derivación se describe aquí sigue siendo válida en la medida en que va. La base para una investigación cuantitativa en las propiedades de los fenómenos del sector cósmica, en en general, es el hecho de que las relaciones de espacio-tiempo se invierten en el nivel de la unidad. Por ejemplo, ''... el propiedad de la masa cósmica inversa se ??observa en el sector de materiales como una masa de magnitud inversa. Cuando un átomo de material tiene una masa de unidades de Z en la escala de número atómico, la correspondiente cósmica átomo tiene una masa inversa de unidades Z que se observa en el sector de material como si se tratara de una masa de 1 / Z unidades. 2 ''Debido a la inversión de tiempo y espacio a nivel de unidad, las frecuencias de la radiación cósmica son la inversa de las de la radiación en el sector de materiales. Estrellas emiten radiación cósmica sobre todo en el infrarrojos, en lugar de sobre todo en las frecuencias ópticas .. y así sucesivamente ''. 3 Por lo tanto, esperamos que el radiación de fondo a estar a una temperatura baja (es decir, alta temperatura inversa). 2.1 Densidad de energía promediada Trataremos para calcular la temperatura de la radiación de fondo mediante la adopción de la energía enfoque de densidad. La densidad de energía en el espacio de radiación de cuerpo negro a una temperatura de T es Kelvin dada por
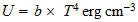 (1)
(1)
donde
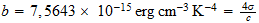 =
=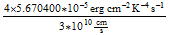 :
:
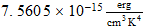
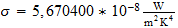 =
=
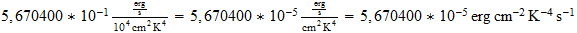
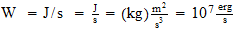
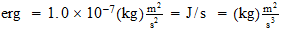
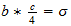
b=
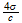 =
=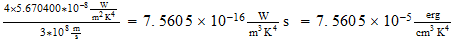
La principal contribución a la radiación de fondo es de las estrellas cósmicas. Por lo tanto, vamos a intentar para llegar a la densidad de energía media de la radiación cósmica estrella mediante la búsqueda de la media de la agrupado densidad de energía de la radiación de todas las estrellas en el sector de material y luego tomar su inversa. En esta coyuntura debemos reconocer un punto de vital importancia que hace que el análisis simple: a un observador en el sector cósmica los átomos en el centro de una estrella sector de material son tanto expuesto como los que están en su periferia, y la radiación de los átomos de interior es tanto observables como que a partir de los átomos de exteriores. Esto se debe a que, como ya se ha mencionado, la ubicación de los átomos de un agregado espacial son al azar y ampliamente dispersos en el marco de referencia temporal en tres dimensiones. Análogamente, a un observador en el sector de materiales se observa todos los átomos de la estrella sector cósmico. Puesto que (i) el temperaturas en el núcleo estelar son más grandes en muchos órdenes de magnitud-casi un mil millones de veces de lo las temperaturas en las regiones exteriores de una estrella y (ii) la densidad de energía es proporcional a la cuarta potencia de la temperatura (Ecuación ( 1)) , se introduce ningún error apreciable si la densidad de energía de la radiación estelar, se originó en un sector, pero como se observa en el sector opuesto, se calcula sobre la base de la temperatura central de solo. 2 Dewey B. Larson, Nothing but Movimiento, Pacífico Norte Pub., 1979, p. 190 3 Dewey B. Larson, El Universo de Movimiento, Pacífico Norte Pub., 1984, p. 387
Página 3
Radiación Cósmica de Fondo 3 La temperatura que reina en el centro de una estrella se determina por la destructiva de la temperatura T d de los elemento más pesado de lo que actualmente está siendo convertida a la radiación mediante la neutralización térmica proceso. En teoría esperamos estrellas ''quemando'', es decir, sometidos a la neutralización térmica -Elementos con números atómicos que van todo el camino desde 117 hasta un valor límite, Z s , Que se produzca. Z s es el número atómico del elemento que, como se explica en detalle en otra parte 4 , Cuando llega a la centro de la estrella, conduce a una cadena de eventos que culmina en la destrucción térmica del grupo de Co / Fe de los elementos, es decir, en el tipo I las explosiones de supernovas. No se quema un elemento con atómica estrellas número menor que Z s es posible, ya que se habría desintegrado en las explosiones de supernovas. Consideraciones teóricas sugieren que Z s podría ser de entre 30 y 26. 4 La densidad de energía correspondiente de la radiación de una estrella ardiente elemento Z en su centro es U z = B \ (T d, z ) 4 ergio cm 3 (2) donde T d, z es el límite destructiva térmica del elemento Z, en grados Kelvin. Ahora se hace necesario para estimar la proporción de cada uno de las estrellas con la temperatura central son la mismo que el límite destructiva del elemento Z, para Z = 117 a la Z s . Desde la más abundante un elemento pasa a ser, cuánto más grande el número de estrellas ardientes que, sobre la base de la abundancia cósmica de los elementos que se tiene que ser uniforme en todo el universo, se puede deducir la relación entre el número de estrellas quema del elemento Z, para el número total de estrellas como F z = un z S (un z ) (3) donde un z es la abundancia cósmica relativa del elemento Z y S () representa, S Z = Z s 117 () Por lo tanto la densidad de energía esperado de la radiación de todas las estrellas se puede dar por U = S (f z U z ) = [ b S (Un z ) ] S (un z (T d, z ) 4 ) ergio cm 3 (4) 2.2 La densidad de energía inversa Debido a la relación recíproca entre las cantidades correspondientes del material y cósmica sectores, la densidad de energía de la radiación de las estrellas cósmicos serían la inversa de esta cantidad. Pero antes de tomar la inversa hay que convertir las cantidades correspondientes a las unidades naturales de la unidades convencionales. Por lo tanto la densidad de energía en unidades naturales es u = U (E n S n -3 ) (5) 4 KVK Nehru, Variables intrínsecas, las supernovas y el límite térmico , Reciprocidad, XVII ? 1, Spring 1988, p. 20.
Página 4
4 Radiación Cósmica de Fondo Donde En = Unidad natural de la energía, expresada en unidades convencionales 5 = 1,49175 \ 10-3 erg y S n = Unidad natural del espacio, expresado en unidades convencionales 5 = 4.558816 x 10.6 cm Tenemos que reconocer ahora que la radiación en el sector cósmico se dispersa en el tiempo de tres dimensiones mientras que el sector de material avanza linealmente en el tiempo de una sola dimensión. Un unidimensional progresión en el sector cósmica tiene dos ''direcciones'' opuestos entre sí en el tiempo (digamos, AB y BA), sólo uno de los cuales es coincidente con la ''dirección'' de la progresión de tiempo el sector de material. El total la radiación cósmica del sector se distribuye por igual entre las dos direcciones temporales y en consecuencia, la densidad de energía aparente para nosotros sería sólo la mitad del total. Es decir u aplicación = u 2 (6) Larson resalta este punto de la relación entre lo real y la aparente luminosidad mientras discutir la radiación quasar. 6 Por último, la densidad de energía de la radiación de las estrellas como cósmicos observado por nosotros es en la inversa de esta cantidad u c = 1 u aplicación = 2 u en unidades naturales (7) 2.3 térmica frente inversa Distribución térmica En esta coyuntura una pregunta que surge naturalmente es que si la naturaleza de esta radiación desde el sector cósmica sería térmica o no. Sobre todo, al recordar lo que se ha citado de Referencia 3 anterior, está claro que esta radiación es de tipo térmico inverso. Bajo estas circunstancias, la adopción de la Ecuación ( 1) i s cuestionable, ya que se refiere sólo a la radiación térmica. Al examinar los valores de los límites destructivos térmicas de los elementos, encontramos a todos más grandes que la temperatura de la unidad, es decir, la temperatura correspondiente a la velocidad de la unidad. 4 Si tenemos en cuenta que el demarcaciones de los rangos de velocidad del sector de material son tanto aplicable a la vibratorio lineal velocidades (agitación térmica) en cuanto a las velocidades de traslación lineal, se hace evidente que el centro de temperaturas de las estrellas del sector materiales están en el rango intermedio, es decir, en el lado de tiempo-cero el rango de una sola dimensión. 7 Citando Larson: ''... la radiación térmica ordinaria se ... producido por la materia a temperaturas inferiores a que corresponde a la velocidad de la unidad. La materia a temperaturas por encima de este nivel produce térmica inversa la radiación por el mismo proceso, ... con una distribución de energía que es la inversa de la normalidad distribución aplicables a la radiación térmica ''. 8 A partir de lo anterior, la siguiente silogismo sugiere en sí: 1. La distribución de la energía de un fenómeno sector cósmica sería la inversa de la energía distribución del fenómeno sector de material correspondiente. 2. El fenómeno bajo consideración es la distribución de la radiación desde el núcleo de un cósmico estrella sector. 5 Dewey B. Larson, Nada más que Motion , Op. cit., p. 160 . 6 Dewey B. Larson, El Universo de Motion , Op. cit., p. 341 . 7 Ibid., La Figura 8, p. 72 . 8 Ibid., p. 246 .
Página 5
Radiación Cósmica de Fondo 5 3. La distribución de la radiación desde el núcleo de una estrella sector de material es térmica inversa, desde se origina en el rango de temperatura intermedia. 4. Por lo tanto la distribución de la radiación desde el núcleo de una estrella sector cósmica sería el inverso de térmica inversa, es decir, térmica. 2.4 Comparación con Observaciones Volviendo a las unidades convencionales, tenemos la densidad aparente de energía de la radiación de fondo como U c = U c (E n S n -3 ) Erg cm -3 (8) Finalmente la temperatura derivado de la radiación de fondo, con la densidad de energía dada por la ecuación (8) está (la adopción de la Ecuación (1) ) T c = ( U c b ) Cuarta K (9) Sustituyendo las ecuaciones (4), (5), (7) y (8) en la ecuación (9) y simplificando T c = 5,4257 \ 10 13 [ S (un z ) S (un z T d, z 4 ) ] Cuarta K (10) La adopción de los valores calculados teóricamente de un z , La abundancia relativa cósmica 9 y T d, z , La térmica límites destructivos 4 de los elementos, la temperatura de fondo T c se elaboran para Z s = 117, 116, ..., 26. La inclusión de un programa Pascal para este cálculo se da en el Apéndice. Algunos de los computarizada valores de T c se enumeran en la Tabla 1 para Z s los valores de 31 a 26. Tabla 1: Valores calculados del Fondo Cósmico de Radiación Temperatura Z s T c (Kelvin) 31 2.989 30 2.798 29 2.614 28 2.435 27 2.587 26 2.739 El candidato más probable para Z s , Ya sea a partir de las consideraciones teóricas 4 o desde la empírica datos de abundancia cósmica resulta ser 30. La temperatura esperada de la radiación de fondo correspondiente a la Z s = 30 puede ser visto a ser 2.798 grados Kelvin. Los valores observados en la literatura rango de 23,74 a 2,9 grados Kelvin. Es instructivo observar que el valor de esta temperatura calculada en la base del elemento de Fe (es decir, Z s = 26) que de acuerdo a Larson es el elemento responsable de 9 KVK Nehru, Abundancia relativa de los Elementos , Reciprocidad, XII ? 3, invierno 1985, p. 28.
Página 6
6 Radiación Cósmica de Fondo la explosión de la supernova, resulta ser 2,74 Kelvin. Esto está en buen acuerdo con el recientemente valor publicado de 2,75 Kelvin estimada a partir de las observaciones precisas. 10 A pesar de que la derivación de la temperatura de la radiación de fondo se describe en este documento es superficial, si es suficiente para demostrar que podría ser derivado de la teoría solo en el contexto del Sistema recíproco. 3 Conclusiones Para poner de relieve algunos de los puntos importantes sacó: 3.1 Las estrellas del sector cósmico del universo físico son agregados en el tiempo y se observan átomo por átomo, se distribuye al azar en el espacio tridimensional. 3.2 La radiación de estos se puede observar como la radiación cósmica de fondo: su absoluta homogeneidad e isotropía resultante de artículo 3.1 anterior. 3.3 El patrón de distribución de esta radiación es inversa de térmica inversa, es decir, térmica. 3.4 Dado que la radiación procedente de las estrellas cósmicas queda igualmente dividido entre los dos ''direcciones'' opuestos de cualquier dimensión de una sola vez, la luminosidad aparente que se observa desde el sistema de referencia espacial de nuestro sector de materiales (que progresa ''unidireccional'' en el tiempo) es la mitad de la luminosidad real. 3.5 La densidad de energía de la radiación de fondo es la densidad de energía aparente de la estrella cósmica la radiación, que es el recíproco de la densidad de energía de la radiación estrella material después de representa el punto 3.4 anterior. 3.6 La temperatura de la radiación de fondo calculado para Z s = 30 es 2.798 Kelvin y para Z s = 26 es 2.739 grados Kelvin (en la que Z s es el número atómico del elemento en el núcleo estelar responsable de Supernova Tipo I). Estos son en estrecho acuerdo con el valor de observación de 2,75 grados Kelvin. 10 David T. Wilkinson, la anisotropía de la radiación de cuerpo negro cósmico, Science, vol. 232, 20 de junio de 1986, pp 1517-1522
Cosmic Background Radiation:
Origin and Temperature
Prof. K.V.K. Nehru, Ph.D.
1 The Cosmic Sector
One of the outstanding achievements of the Reciprocal System of theory is the discovery of the fact
that the physical universe is not limited to our familiar world of three dimensions of space and one
dimension of time, the material sector as Larson calls it. By virtue of the symmetry between the
intrinsic natures of space and time, brought to light by Larson, he demonstrates the existence of a
cosmic sector of the physical universe, wherein space-time relations are inverse of those germane to the
material sector.
The normal features of the cosmic sector could be represented in a fixed three-dimensional temporal
reference frame, just as those of the material sector could be represented in a fixed, three-dimensional
spatial reference frame. In the universe of motion, the natural datum on which the physical universe is
built is the outward progressional motion of space-time at unit speed (which is identified as the speed
of light). The entities of the material sector are the result of downward displacement from the
background speed of unity (speeds less than unity), while those of the cosmic sector are the result of
upward displacement from unit (speeds greater than unity). But entities.like radiation.that move at
the unit speed, being thereby at the boundary between the two sectors, are phenomena that are common
to both these sectors.
Gravitation, being always in opposition to the outward space-time progression, is inward in scalar
direction in the three-dimensional spatial or temporal reference frames. Since independent motion in
the material sector (three-dimensional space) is motion in space, gravitation in our sector acts inward in
space and results in large-scale aggregates of matter. Gravitation in the cosmic sector acts still inward
but it is inward in three-dimensional time rather than in space. Consequently the cosmic sector
equivalents of our stars and galaxies are aggregates in time rather than in space.
Further, as Larson points out, gcthe various physical processes to which matter is subject alter
positions in space independently of positions in time, and vice versa. As a result, the atoms of a
material aggregate, which are contiguous in space, are widely dispersed in time, while the atoms of a
cosmic aggregate, which are contiguous in time, are widely dispersed in spacec
gRadiation moves at unit speed relative to both types of fixed reference systems, and can
therefore be detected in both sectors regardless of where it originates. Thus we receive
radiation from cosmic stars and other cosmic objects just as we do from the corresponding
material aggregates. But these cosmic objects are not aggregates in space. They are
randomly distributed in the spatial reference system. Their radiation is therefore received in
space at a low intensity and in an isotropic distribution. Such a background radiation is
actually being received.h1
1 Dewey B. Larson, The Neglected Facts of Science, North Pacific Pub., Oregon, U.S.A, 1982, pp. 72-73.
Reciprocity 19 4 page 20 Copyright c2012 by ISUS, Inc. All rights reserved. Rev. 4
2 Cosmic Background Radiation
2 The Radiation Temperature
An approach to the derivation of the temperature of this cosmic background radiation is described now.
This can be seen to involve the consideration of several other previously derived items like the relative
cosmic abundances of the elements and their thermal destructive limits. To this extent, therefore, the
present analysis has to be treated as provisional.a revision in the derivation of these items would
entail a corresponding modification in the present derivation. Notwithstanding this, the general
approach to the derivation described herein continues to be valid as far as it goes.
The basis for a quantitative inquiry into the properties of the phenomena of the cosmic sector, in
general, is the fact that the space-time relations are inverted at the unit level. For instance, gcthe
cosmic property of inverse mass is observed in the material sector as a mass of inverse magnitude.
Where a material atom has a mass of Z units on the atomic number scale, the corresponding cosmic
atom has an inverse mass of Z units which is observed in the material sector as if it were a mass of 1/Z
units.2
gBecause of the inversion of space and time at the unit level, the frequencies of the cosmic radiation are
the inverse of those of the radiation in the material sector. Cosmic stars emit radiation mainly in the
infrared, rather than mainly at the optical frequencies .. and so on.h3 Therefore, we expect the
background radiation to be at a low temperature (that is, high inverse temperature).
2.1 Averaged Energy Density
We shall attempt to calculate the temperature of the background radiation by adopting the energy
density approach. The energy density in space of blackbody radiation at a temperature of T Kelvin is
given by
U=b~T4 erg
cm3 (1)
where b = 7.5643~10-15 erg-cm-3 K-4.
The major contribution to the background radiation is from the cosmic stars. As such, we shall attempt
to arrive at the average energy density of the cosmic star radiation by finding the lumped average of the
energy density of the radiation from all the stars in the material sector and then taking its inverse. At
this juncture we should recognize a point of crucial importance which renders the analysis simple: to an
observer in the cosmic sector the atoms at the center of a material sector star are as much exposed as
the ones at its periphery, and the radiation from the interior atoms is as much observable as that from
the outer atoms. This is because, as already mentioned, the locations of the atoms of a spatial aggregate
are randomly and widely dispersed in the three-dimensional temporal reference frame. Analogously, to
an observer in the material sector all the atoms of the cosmic sector star are observable. Since (i) the
temperatures in the stellar core are larger by many orders of magnitude.nearly a billion times.than
the temperatures in the outer regions of a star and (ii) energy density is proportional to the fourth power
of temperature (Equation (1)), no appreciable error would be introduced if the energy density of the
stellar radiation, originated in one sector but as observed in the opposite sector, is calculated on the
basis of the central temperature alone.
2 Dewey B. Larson, Nothing but Motion, North Pacific Pub., 1979, p. 190
3 Dewey B. Larson, The Universe of Motion, North Pacific Pub., 1984, p. 387
Cosmic Background Radiation 3
The temperature prevailing at the center of a star is determined by the destructive temperature Td of the
heaviest element in it that is currently getting converted to radiation by the thermal neutralization
process. On theoretical grounds we expect stars gburningh.that is, undergoing thermal neutralization
.elements with atomic numbers ranging all the way from 117 down to a limiting value, Zs, to occur. Zs
is the atomic number of the element which, as explained in detail elsewhere4, when it arrives at the
center of the star, leads to a chain of events culminating in the thermal destruction of the Co/Fe group
of elements, in other words, in Type I supernova explosions. No star burning an element with atomic
number less than Zs is possible because it would have disintegrated in the supernova explosions.
Theoretical considerations suggest that Zs could be between 30 and 26.4 The relevant energy density of
the radiation of a star burning element Z at its center is
Uz=b~(T d , z)4 erg
cm3 (2)
where Td,z is the thermal destructive limit of element Z, in kelvin.
Now it becomes necessary to estimate the proportion each of the stars with central temperature are the
same as the destructive limit of the element Z, for Z = 117 to Zs. Since the more abundant an element
happens to be, the larger would be the number of stars burning it, on the basis of the cosmic abundance
of the elements that is taken to be uniform throughout the universe, we can deduce the ratio of the
number of stars burning element Z to the total number of stars as
f z=
az
S (a z)
(3)
where az is the relative cosmic abundance of element Z and S( ) stands for,
°
Z=Z s
117
()
Hence the expected energy density of the radiation from all the stars can be given by
U=S ( f zU z)
=[bS
(a z)]S (az (Td , z)4) erg
cm3
(4)
2.2 The Inverse Energy Density
Because of the reciprocal relationship between corresponding quantities of the material and cosmic
sectors, the energy density of the radiation from the cosmic stars would be the inverse of this quantity.
But before taking the inverse we must convert the concerned quantities into the natural units from the
conventional units. Thus the energy density in natural units is
u= U
(En Sn . 3)
(5)
4 K.V.K. Nehru, Intrinsic Variables, Supernovae and the Thermal Limit, Reciprocity, XVII 1, Spring 1988, p. 20.
4 Cosmic Background Radiation
Where En = natural unit of energy expressed in conventional units5 = 1.49175~10-3 erg
and Sn = natural unit of space expressed in conventional units5 = 4.558816~10-6 cm
We need to recognize now that radiation in the cosmic sector is dispersed in three-dimensional time
whereas the material sector progresses linearly in one-dimensional time. A one-dimensional
progression in the cosmic sector has two mutually opposite gdirectionsh in time (say, AB and BA), only
one of which is coincident with the gdirectionh of the time progression of the material sector. The total
radiation from the cosmic sector is distributed equally between the two temporal directions and
consequently the energy density apparent to us would be only half of the total. That is
uapp=u2
(6)
Larson brings out this point of the relationship between the actual and the apparent luminosities while
discussing the quasar radiation.6 Finally, the energy density of the radiation from the cosmic stars as
observed by us is in the inverse of this quantity
uc= 1
uapp
=2u
in natural units (7)
2.3 Thermal versus Inverse Thermal Distribution
At this juncture a question that naturally arises is that whether the nature of this radiation from the
cosmic sector would be thermal or not. Especially, recalling what has been quoted from Reference 3
earlier, it is clear that this radiation is of the inverse thermal type. Under these circumstances the
adoption of Equation (1) is questionable since it pertains only to thermal radiation.
On examining the values of the thermal destructive limits of the elements, we find them all larger than
the unit temperature, that is, the temperature corresponding to unit speed.4 If we remember that the
demarcations of the speed ranges of the material sector are as much applicable to the linear vibratory
speeds (thermal motion) as to the linear translational speeds, it becomes apparent that the central
temperatures of the material sector stars are in the intermediate range, that is, on the time-zero side of
the one-dimensional range.7
Quoting from Larson: gcordinary thermal radiation isc produced by matter at temperatures below
that corresponding to unit speed. Matter at temperatures above this level produces inverse thermal
radiation by the same process,c with an energy distribution that is the inverse of the normal
distribution applicable to thermal radiation.h8
From the foregoing the following syllogism suggests itself:
1. The energy distribution of a cosmic sector phenomenon would be the inverse of the energy
distribution of the corresponding material sector phenomenon.
2. The phenomenon under consideration is the distribution of radiation from the core of a cosmic
sector star.
5 Dewey B. Larson, Nothing But Motion, op. cit., p. 160.
6 Dewey B. Larson, The Universe of Motion, op. cit., p. 341.
7 Ibid., Figure 8, p. 72.
8 Ibid., p. 246.
Cosmic Background Radiation 5
3. The distribution of the radiation from the core of a material sector star is inverse thermal, since
it originates in the intermediate temperature range.
4. Hence the distribution of the radiation from the core of a cosmic sector star would be the
inverse of inverse thermal, that is, thermal.
2.4 Comparison with Observations
Reverting to the conventional units, we have the apparent energy density of the background radiation as
Uc=uc( En Sn .3)erg-cm.3 (8)
Finally the derived temperature of the background radiation, with the energy density given by Equation
(8) is (adopting Equation (1))
Tc=(Uc
b )1/ 4
K (9)
Substituting from Equations (4), (5), (7) and (8) in Equation (9) and simplifying
Tc=5.4257~1013[ S(az)
S (azT d , z
4 ) ]1/4
K (10)
Adopting the theoretically calculated values of az, the relative cosmic abundance9 and Td,z, the thermal
destructive limits4 of the elements, the background temperature Tc are worked out for Zs = 117, 116,c ,
26. The listing of a Pascal program for this calculation is given in the Appendix. Some of the computed
values of Tc are listed in Table 1 for Zs values ranging from 31 to 26.
Table 1: Computed Values of the Cosmic Background Radiation Temperature
Zs Tc (Kelvin)
31 2.989
30 2.798
29 2.614
28 2.435
27 2.587
26 2.739
The most probable candidate for Zs, either from the theoretical considerations4 or from the empirical
cosmic abundance data turns out to be 30. The expected temperature of the background radiation
corresponding to Zs = 30 can be seen to be 2.798 Kelvin. The observed values reported in the literature
range from 23.74 to 2.9 Kelvin. It is instructive to note that the value of this temperature calculated on
the basis of the element Fe (that is, Zs = 26) which according to Larson is the element responsible for
9 K.V.K. Nehru, Relative Abundance of the Elements, Reciprocity, XII 3, Winter 1985, p. 28.
6 Cosmic Background Radiation
the supernova explosion, turns out to be 2.74 Kelvin. This is in fair agreement with the recently
published value of 2.75 Kelvin estimated from accurate observations.10 Even though the derivation of
the temperature of the background radiation described herein is cursory, if suffices to demonstrate that
it could be derived from theory alone in the context of the Reciprocal System.
3 Conclusions
To highlight some of the important points brought out:
3.1 The stars of the cosmic sector of the physical universe are aggregates in time and are observed
atom by atom, being randomly distributed in the three-dimensional space.
3.2 The radiation from these is observable as the cosmic background radiation: its absolute
uniformity and isotropy resulting from item 3.1 above.
3.3 The distribution pattern of this radiation is inverse of inverse thermal, that is, thermal.
3.4 Since the radiation originating from the cosmic stars gets equally divided between the two
opposite gdirectionsh of any single time dimension, the apparent luminosity as observed from
the spatial reference system of our material sector (which progresses gunidirectionallyh in time)
is half of the actual luminosity.
3.5 The energy density of the background radiation is the apparent energy density of the cosmic star
radiation, which is the reciprocal of the energy density of the material star radiation after
accounting for item 3.4 above.
3.6 The temperature of the background radiation computed for Zs = 30 is 2.798 Kelvin and for Zs =
26 is 2.739 Kelvin (where Zs is the atomic number of the element at stellar core responsible for
Type I supernova). These are in close agreement with the observational value of 2.75 Kelvin.
10 David T. Wilkinson, Anisotropy of the Cosmic Blackbody Radiation, Science, Vol. 232, 20 June 1986, pp. 1517-1522.
Cosmic background radiation
Radiacion de fondo cosmico
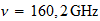
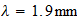
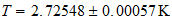
Calculate the relationship between temperature and absolute Hartrees
Calculemos
la relacion entre hartrees y la temperatura absoluta

Hartrees calculate the corresponding temperature for cosmic background
Calculemos las hartrees correspondientes para la temperatura de fondo cosmico
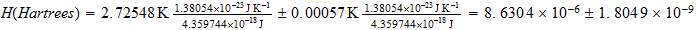
Compute the corresponding inverse temperature in the cosmic sector or Counterspace
Calculemos la temperatura inversa correspondiente en el sector cosmico o contraespacio
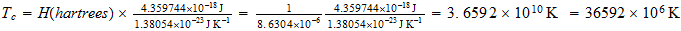
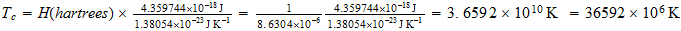
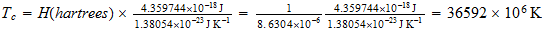
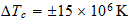
---------------------------------------------------------
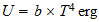
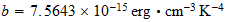
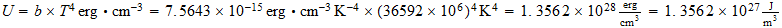
----------------------------------------------------------------------
Temperatura
del punto unidad
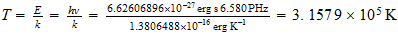
Relacion con la temperatura del fondo cosmico
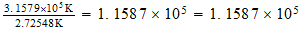
Relacion inversa
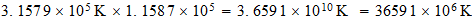
36 mil millones de grados
http://www.astroscu.unam.mx/~wlee/OC/SSAAE/AAE/Supernovas/Explosion%20de%20supernova.html
http://www.scienceinschool.org/print/528
Página
Cuando este material nuclear se agota la temperatura y presión de la estrella
aumenta de forma notable hasta que comienza a formar ...En ese momento su
temperatura nuclear puede ser de 70 mil millones de grados y cuando agota el
Hierro la estrella se vuelve inestable y ... El fenómeno de la explosión de una
supernova es similar al de la explosión de una Nova, pero con la diferencia
sustancial de ...
http://books.google.es/books?id=Klc_JmXMF_8C&pg=PT18&lpg=PT18&dq=temperatura+en+las+explosiones+termonucleares+de+las+supernovas+millones+de+grados&source=bl&ots=I-nspfHNXs&sig=VF4OH203XTaSjaRH0U5yA18mOyI&hl=es&sa=X&ei=2FP3Upn0Js3M0AW_IA&ved=0CEwQ6AEwBQ#v=onepage&q=temperatura%20en%20las%20explosiones%20termonucleares%20de%20las%20supernovas%20millones%20de%20grados&f=false
books.google.es/books?isbn=8468609544
----------------------------------------------------------------------------------
Frecuencia
Fondo Cosmico:

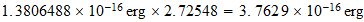
Frecuencia
Unidad:
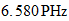
Frecuencia inversa del Fondo Cosmico:
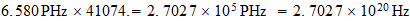
Energia liberada en la fision:
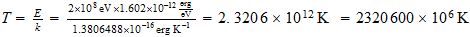
-------------------------------------------------------------------------------------------------------------------------
repeticion
Temperatura del punto unidad
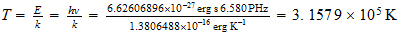
Relacion con la temperatura del fondo cosmico
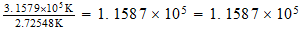
Relacion inversa
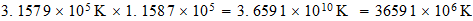
----------------------------------------------------------------------------------
Frecuencia
Fondo Cosmico:
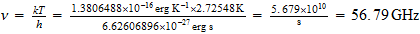
Esta
frecuencia del fondo cosmico se obtiene no solo por la aplicacion de la
anterior ecuacion sino tambien por la simple proporcionalidad inversa que
habiamos obtenido anteriormente entre temperatura unidad y temperatura del
fondo cosmico .
Frecuencia Unidad:
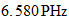
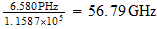
Frecuencia inversa del Fondo Cosmico:
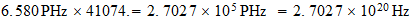
------------------------------------------------------------
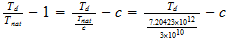
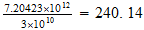
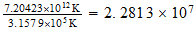
b) --------------
Espectro electromagnetico&radiacion de fondo cosmico
contraespacio o espacio rotacional
 |
 Radiacion
de fondo cosmico en Radiacion
de fondo cosmico en
 |
||||||||||||
espacio
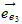 |
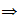 ?
en ?
en
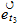 |
(*) Temperatura limite destructiva maximas, para los diferentes grupos de elementos quimicos
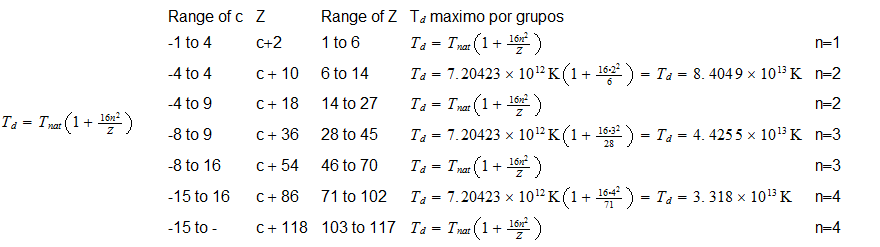
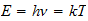
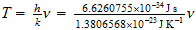
Como obtener de forma teorica a traves del Sistema Reciproco la masa de un elemento quimico coincidiendo con la masa empirica.
Energía de Enlace Nuclear =
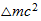
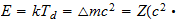 masa
proton+
masa
proton+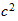 masa
neutron)
masa
neutron)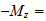
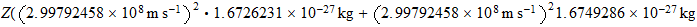 )
)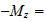
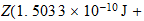
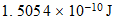 )
)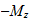
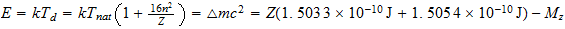
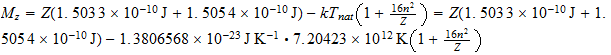
En el caso del hierro
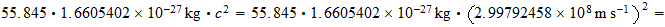
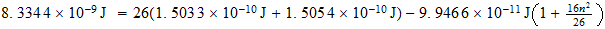 ,
Solution is :
,
Solution is :
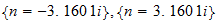
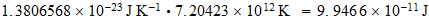
b) -----------------------------------
For obtaining of cosmic background radiation, Nehru used Tnat, but I think you should use T (3base) or T (effective). Larson cited in:
http://www.reciprocalsystem.com/bpm/bpm05.htm
Para la obtencion de la radiacion de fondo cosmico, Nerhu utiliza Tnat, pero creo que se deberia utilizar T(3base) o bien T(efectiva). Que cita Larson en:
http://www.reciprocalsystem.com/bpm/bpm05.htm
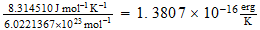
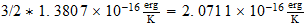
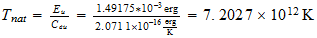
T(3
base)=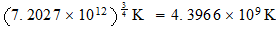
T (efectiva)=
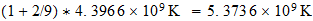
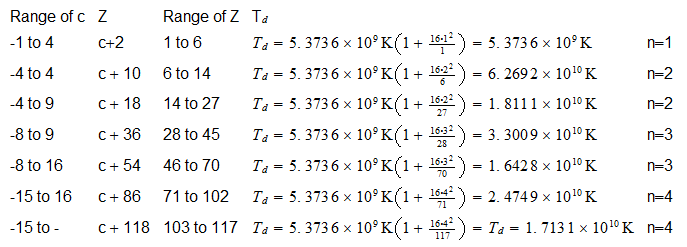
--------------------------------------
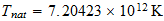

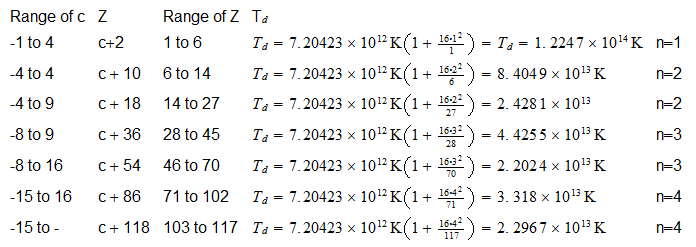
Energía de Enlace Nuclear
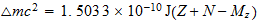
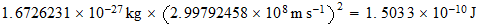
Si la igualamos a la energia destructiva del Sistema Reciproco
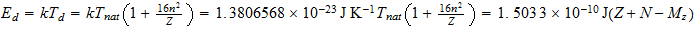
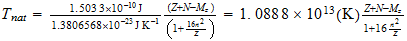
Peso
atomico
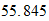
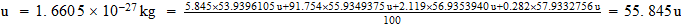
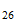 Fe
Fe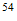
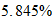
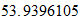
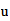
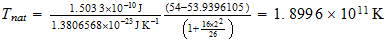
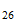 Fe
Fe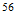
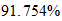
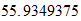
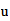
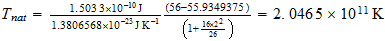
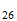 Fe
Fe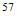
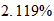
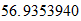
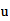
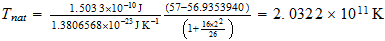
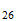 Fe
Fe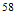
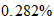
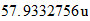
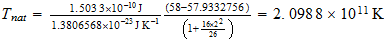
Restos.-
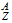 X
X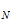
Peso atomico
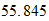
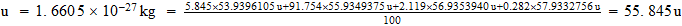
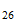 Fe
Fe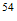
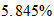
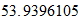
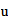
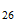 Fe
Fe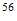
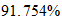
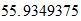
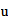
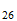 Fe
Fe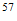
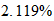
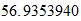
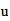
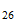 Fe
Fe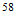
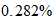
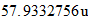
American Journal of Physics
-----------------------------------------------------
Espectro Electromagnetico
?
Octavas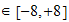
Octava
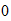
Espectro electromagnetico
3 dimensiones
20 grados de libertad
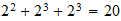
Combinaciones
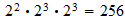
Valores no degenerados
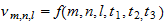
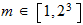
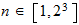
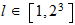
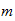 ,
,
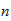 ,
,
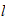
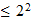
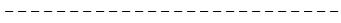
Inter-regional
Ratio (R)
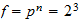
f=Grados de libertad
p=posibilisibilidades por dimension
n=dimensiones
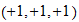
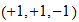
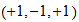
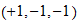
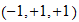
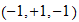
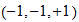
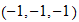
Unit space (s):
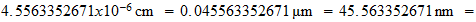
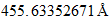
Unit time (t) :
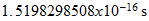
Unit speed (s/t):
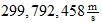 (exact)
(exact)
Inter-regional Ratio (R):
Atomic rotation:
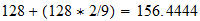
Subatomic rotation:
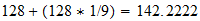
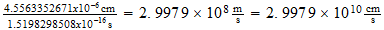
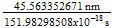
------------------------------------------------------------------------------------------
9.-- TABLA ELEMENTOS QUIMICOS
-----------------------------------------
Atomic Number Equation Based on Larsons Triplets
David Halprin
Where Z represents the Atomic Number, and (a, b, c) is the number triplet representing the atoms:
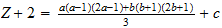
If a = b then this reduces to
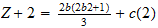
If a = b + 1 then it reduces to
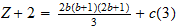
a=b a = b+1
a b a b Range of c Z Range of Z
2 1 -1 to 4 c + 2 1 to 6
2 2 -4 to 4 c + 10 6 to 14
3 2 -4 to 9 c + 18 14 to 27
3 3 -8 to 9 c + 36 28 to 45
4 3 -8 to 16 c + 54 46 to 70
4 4 -15 to 16 c + 86 71 to 102
5 4 -15 to -1 c + 118 103 to 117
Equation (1) is exactly representative of Deweys algorithm.
Equations (2) and (3) are just simplifications of Equation (1) when a = b and a = b + 1 respectively.
Some specific examples:
Larsonium1
5-4-(1) substituted into Equation (3) gives Z = 117 as expected, however there is an
interesting aside to consider, despite its counter-intuitive appearance and it requires some interpretation
within RS too.
1 Not an official name for the element; also identified as Farnsium in Futurama episode, Near-Death Wish.
Copyright ©2002 by ISUS, Inc. All rights reserved.2 Atomic Number Equation Based on Larsons Triplets
Atom /
Particle
Atomic Number
a-b-c Z
0-0-(1) -3
Electron 1-0-(1) -3
Rotational base
1-0-0 -2
0-0-0 -2
0-0-1 -1
Positron 1-0-1 -1
Neutrino 1-1-(1) -1
Neutron 1-1-0 0
Deuteron 1-1-0 0
Alpha Particle 1-1-0 0
Deuterium 1-1-1 1
----------------------------------
TablaElementos Quimicos
TABLA ELEMENTOS QUIMICOS
H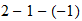 |
He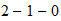 |
||||||||||||||||
9.- MECANICA CUANTICA
2.2 Matter Waves
says
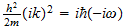
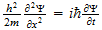 (14)
(14)
should say
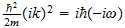
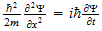
Page 1
''Mecánica Cuántica''
Como la Mecánica de la región de tiempo
Prof. KVK Nehru, Ph. D
Los resultados preliminares de un estudio crítico de la mecánica
ondulatoria realizadas a la luz de la el conocimiento de la teoria del sistema
recíproco ya se ha informado
anteriormente .
Parte de su importancia los resultados son los siguientes. Si bien la
mecánica ondulatoria ha tenido mucho éxito matemáticamente, es
contiene algunos errores fundamentales. El principal escollo ha sido el
desconocimiento de la existencia de la región de tiempo y sus
características peculiares. Los puntos cruciales que deben ser reconocido
son que la onda asociada con una partícula en movimiento, en un sistema
de dimensiones atómicas, existe en el espacio equivalente de la
región de tiempo, y que el cambio de la concepción de
partículas a la ola vista es igual en importancia al desplazamiento del
punto de vista de la referencia espacial en tres dimensiones enmarcar a que el
marco de referencia temporal tridimensional que es pertinente a la región
de tiempo. A imaginar que incluso los objetos brutos tienen una onda asociada
con ellos es un error: la cuestión de la ola no se plantea a menos que
los fenómenos preocupados entrar en la región el tiempo. Un
corolario es que los teóricos de la hipótesis de que la onda
asociada a la partícula en movimiento es espacialmente co-extensiva con
la partícula es incorrecto ya que la primera existe en el espacio
equivalente, no en el espacio de ampliación del sistema de referencia
espacial convencional. El principio de incertidumbre se debe a la
theorists'practice de recurrir a paquetes de ondas. Además, se ha
demostrado que la connotación de probabilidad de la función de onda
surge de los dos hechos que la onda es existente en el colector temporal de
tres dimensiones, y que las localizaciones en la colector temporal
tridimensional sólo se conectan al azar a los lugares en los tres
colector espacial tridimensional. La naturaleza no local de las fuerzas
(movimientos) en la región el tiempo también se desprende de estos
hechos. Cálculos basados ??en las relaciones inter-regionales aplicables
confirman la afirmación de Larson que la miden tamaño del átomo
está en el intervalo femtometer y por lo tanto lo que se encuentra a
partir de los experimentos de dispersión es el tamaño del átomo
en sí-no de un núcleo. A partir de dicho estudio se hizo claro que
los comentarios de los críticos de que el mundo a pequeña escala no
es intrínsecamente racional y que la teoría cuántica no puede
entenderse intuitivamente fueron erróneamente fundada. Lo que realmente
falta es el conocimiento de la existencia y características de la
época región, la región interior de la unidad natural del
espacio, donde sólo es posible el movimiento en el tiempo. Desde nuestra
conocimiento del sistema recíproco ayudó a arreglar algunos de los
problemas conceptuales de la ola Mecánica y ha señalado que su
fundamento original ha sido con razón (aunque inconscientemente) fundada,
un se ha hecho intento de indagar en sus aspectos matemáticos con el fin
de ver si son válidos en la luz de nuestra comprensión del sistema
recíproco. Los resultados de esta investigación se presentan en este
artículo. 1 KVK Nehru, ''la mecánica ondulatoria de la luz del
sistema de reciprocidad,'' Reciprocidad, vol. XXII, N
.
Parte de su importancia los resultados son los siguientes. Si bien la
mecánica ondulatoria ha tenido mucho éxito matemáticamente, es
contiene algunos errores fundamentales. El principal escollo ha sido el
desconocimiento de la existencia de la región de tiempo y sus
características peculiares. Los puntos cruciales que deben ser reconocido
son que la onda asociada con una partícula en movimiento, en un sistema
de dimensiones atómicas, existe en el espacio equivalente de la
región de tiempo, y que el cambio de la concepción de
partículas a la ola vista es igual en importancia al desplazamiento del
punto de vista de la referencia espacial en tres dimensiones enmarcar a que el
marco de referencia temporal tridimensional que es pertinente a la región
de tiempo. A imaginar que incluso los objetos brutos tienen una onda asociada
con ellos es un error: la cuestión de la ola no se plantea a menos que
los fenómenos preocupados entrar en la región el tiempo. Un
corolario es que los teóricos de la hipótesis de que la onda
asociada a la partícula en movimiento es espacialmente co-extensiva con
la partícula es incorrecto ya que la primera existe en el espacio
equivalente, no en el espacio de ampliación del sistema de referencia
espacial convencional. El principio de incertidumbre se debe a la
theorists'practice de recurrir a paquetes de ondas. Además, se ha
demostrado que la connotación de probabilidad de la función de onda
surge de los dos hechos que la onda es existente en el colector temporal de
tres dimensiones, y que las localizaciones en la colector temporal
tridimensional sólo se conectan al azar a los lugares en los tres
colector espacial tridimensional. La naturaleza no local de las fuerzas
(movimientos) en la región el tiempo también se desprende de estos
hechos. Cálculos basados ??en las relaciones inter-regionales aplicables
confirman la afirmación de Larson que la miden tamaño del átomo
está en el intervalo femtometer y por lo tanto lo que se encuentra a
partir de los experimentos de dispersión es el tamaño del átomo
en sí-no de un núcleo. A partir de dicho estudio se hizo claro que
los comentarios de los críticos de que el mundo a pequeña escala no
es intrínsecamente racional y que la teoría cuántica no puede
entenderse intuitivamente fueron erróneamente fundada. Lo que realmente
falta es el conocimiento de la existencia y características de la
época región, la región interior de la unidad natural del
espacio, donde sólo es posible el movimiento en el tiempo. Desde nuestra
conocimiento del sistema recíproco ayudó a arreglar algunos de los
problemas conceptuales de la ola Mecánica y ha señalado que su
fundamento original ha sido con razón (aunque inconscientemente) fundada,
un se ha hecho intento de indagar en sus aspectos matemáticos con el fin
de ver si son válidos en la luz de nuestra comprensión del sistema
recíproco. Los resultados de esta investigación se presentan en este
artículo. 1 KVK Nehru, ''la mecánica ondulatoria de la luz del
sistema de reciprocidad,'' Reciprocidad, vol. XXII, N
 2, Otoño 1993, p. 8-13. Reciprocidad 24 ? 1 página 1, Revisado
2/1998 Copyright © 1995 por ISUS, Inc. Todos los derechos reservados.
Rev. 47
2, Otoño 1993, p. 8-13. Reciprocidad 24 ? 1 página 1, Revisado
2/1998 Copyright © 1995 por ISUS, Inc. Todos los derechos reservados.
Rev. 47
Página 2
1 ¿Dónde estamos Antes de seguir adelante,
Sería conveniente tener un balance de la situación atómica desde el punto de vista del sistema recíproco. En primer lugar, Larson 2 afirma que el átomo es sin partes, que es una unidad de movimiento compuesto, movimiento siendo el elemento básico del universo físico. Esto significa que tanto en el núcleo y la llamada electrones orbitales son inexistentes. En segundo lugar, sostiene que no hay una fuerza eléctrica o bien, que participan en la estructura atómica. Este, Por lo tanto, las hojas de la gravitación y la progresión espacio-tiempo como los únicos dos movimientos (fuerzas) que los operar dentro de la región de tiempo con, por supuesto, las modificaciones apropiadas peculiares a la región de tiempo introducido en ellos. Bajo estas circunstancias, la cuestión de una fuerza ''nuclear'' no surge en absoluto. Pero es perfectamente legítimo preguntar qué fuerzas (movimientos) se encuentran por una partícula cuando se aproxima a la zona del un átomo, y, de hecho, ya que entra en la propia muy átomo. Igualmente importante es investigar la mecánica del proceso inverso de la emisión de una partícula por el átomo.
2 La ecuación de onda
El punto de partida fundamental para el tratamiento matemático de la
mecánica cuántica es la ecuación de onda. Las ecuaciones de
onda en la teoría cuántica gobiernan las funciones de onda asociadas
con las partículas, y corresponden a las leyes de la mecánica
clásica de Newton. De nuestro estudio anterior tenemos visto que el
cambio de la imagen de partícula a la imagen de onda es una estrategia
legítima que necesita ser adoptada al entrar en la región de tiempo,
ya que es equivalente a pasar de la convencional de tres sistema de referencia
espacial tridimensional de la región del espacio-tiempo de lo temporal en
tres dimensiones marco de referencia de la región de tiempo. Por lo
tanto, el siguiente paso lógico es examinar cómo el gobierno
ecuaciones de los fenómenos ondulatorios han llegado a ver si está
en consonancia con la Sistema recíproco. Puesto que siempre es posible
constituir una onda de cualquier forma por superposición de diferentes
ondas sinusoidales de longitudes de onda y frecuencias adecuadas, limitaremos
nuestra discusión a estos elementales las ondas sinusoidales. La
relación entre el número de onda k y ? la longitud de onda, por un
lado, y que entre la frecuencia angular ? y ? frecuencia en el otro, son como
sigue: k = 2p ? ; O = 2p ? (1) La velocidad de la onda u está dado por u
= ?
 ? = ? k (2) Las formas funcionales generales de las ondas sinusoidales
están sen (kx \ ? t) cos (kx \ ? t) } (3) 2 Larson, Dewey B., El caso
contra el Átomo Nuclear , North Publishers Pacífico, Oregon, EE.UU.,
1963.
? = ? k (2) Las formas funcionales generales de las ondas sinusoidales
están sen (kx \ ? t) cos (kx \ ? t) } (3) 2 Larson, Dewey B., El caso
contra el Átomo Nuclear , North Publishers Pacífico, Oregon, EE.UU.,
1963.
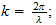
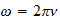
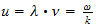
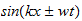
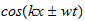
Página 3
y en forma exponencial compleja (véase el Apéndice I: Relación
de Euler ) e i (kx \ ? t) (4) donde la unidad imaginaria i se define por i 2 =
-1. Funciones complejas implican una parte real y una parte imaginaria. Dado
que en esta etapa de nuestro examen del la naturaleza de la función de
onda de las partículas es todavía desconocido, no hay ninguna
razón teórica para excluir funciones complejas. Tengamos en cuenta
que el criterio de juicio es lo que es posible en el tiempo región, no lo
que es posible en la región del espacio-tiempo. Sin duda, cantidades
observables en el tiempo-espacio región debe ser real. Sin embargo, en
virtud de la segunda relación de potencia entre el correspondiente
cantidades en la región de tiempo y de la región del espacio-tiempo,
el valor de una cantidad observable región de tiempo todavía
sería real, incluso si fuera a ser imaginario en la región de tiempo
(por ejemplo, una cantidad i
 ? en el momento región aparecería como (i
? en el momento región aparecería como (i
 ?) 2 , Es decir,-? 2 en la región exterior).
?) 2 , Es decir,-? 2 en la región exterior).
2.1 Ondas de radiación
Vamos a obtener la ecuación que rige para la onda que se propaga a una
velocidad constante, al igual que la de la radiación. En primer lugar se
observa la relación entre el impulso p de la onda y el número de
onda k, y la energía E y su frecuencia angular ?, p = ? k, E = ? ? (5)
donde h es la constante de Planck h dividida por 2p. A partir de la
relación energía-impulso de la ola, p 2 c 2 = E 2 , (C es la
velocidad de la onda constante) que tener p 2 = 1 c 2 E 2 , ? 2 k 2 = 1 c 2 ?
2 ? 2 , k 2 = 1 c 2 ? 2 (6) Suponiendo que la forma de onda más simple,
la de una onda sinusoidal, se escribe en la función de onda compleja
forma exponencial ? (x, t) = A
 correo i (kx-? t) (7) donde A es una constante arbitraria. Para una
función de este tipo, ? ? ? x Ik =
correo i (kx-? t) (7) donde A es una constante arbitraria. Para una
función de este tipo, ? ? ? x Ik =
 ? ? ? ? t = - I ?
? ? ? ? t = - I ?
 ? } (8) Eso es, tomando la derivada con respecto a x es equivalente a
multiplicar por ik, y teniendo la derivada con respecto al tiempo t es
equivalente a multiplicar por - i ?. Así
? } (8) Eso es, tomando la derivada con respecto a x es equivalente a
multiplicar por ik, y teniendo la derivada con respecto al tiempo t es
equivalente a multiplicar por - i ?. Así
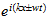
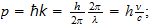
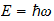
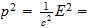
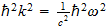
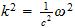
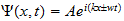
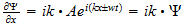
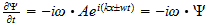
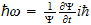
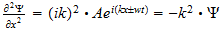
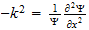
Quantum Mechanics
2.1 Radiation Waves
says
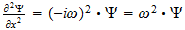
should say (9)
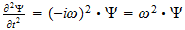
2.2
Matter Waves
says
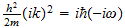
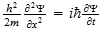 (14)
(14)
should say
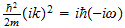
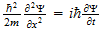
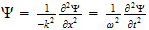
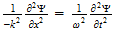
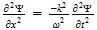
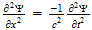
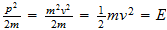
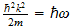
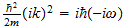
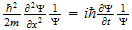
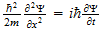
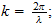
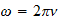
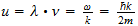
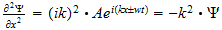
Página 4
? 2 ? ? x 2 = (Ik) 2
 ? = - k 2
? = - k 2
 ? ? 2 ? ? x 2 = (- I ?) 2
? ? 2 ? ? x 2 = (- I ?) 2
 ? = ?- 2
? = ?- 2
 ? } (9) Sustituyendo esto en la última de la ecuación (6 ) se
obtiene ? 2 ? ? x 2 = 1 c 2 ? 2 ? ? t 2 (10) que es exactamente la
ecuación de onda que buscamos (ver Apéndice II: La ecuación
general de un Wave velocidad constante) .
? } (9) Sustituyendo esto en la última de la ecuación (6 ) se
obtiene ? 2 ? ? x 2 = 1 c 2 ? 2 ? ? t 2 (10) que es exactamente la
ecuación de onda que buscamos (ver Apéndice II: La ecuación
general de un Wave velocidad constante) .
2.2 ondas de materia
En el ejemplo de su mentor
Peter Debye, Erwin Schrödinger realizó un estudio detallado de la
ola hipótesis defendida en 1924 por de Broglie. Schrödinger
señaló que la relación energía-momento de una
partícula libre (no se hubiere pronunciado por fuerzas) de masa m p 2 2 m
= E (11) conduce a la relación de frecuencia-número de onda angular
? 2 k 2 2 m = ?
 ? (12) De las ecuaciones (2) y ( 12) w e ver que la velocidad de la onda en
este caso viene dado por u = ? k 2 m (13) Por lo tanto la velocidad de las
ondas de la materia no es constante como la de las ondas de radiación,
pero es un función del número de onda k. la ecuación (12)
podría ser reorganizado como - h 2 2 m (Ik) 2 = I ? (- i ?) Multiplicando
ambos lados por ?, a la vez que podemos ver a partir de las ecuaciones (8) y (
9) que - H 2 2 m ? 2 ? ? x 2 = I ? ? ? ? t (14) que es la ecuación que
rige para la onda asociada a la partícula libre que estamos buscando.
Esta es la ecuación de Schrödinger para la partícula libre. Es
la ecuación en la región de tiempo que corresponde a la primera ley
de la región del espacio-tiempo de Newton. Con el fin de incluir las
interacciones de las partículas con el medio ambiente se observa que la
energía total del como una partícula se compone de la energía
cinética y la energía potencial. Este último podría ser
tomado como sólo depende de la posición y representado por una
función de energía potencial V (x). Así, para un conservador
sistema que tenemos la energía constante E total dado por
? (12) De las ecuaciones (2) y ( 12) w e ver que la velocidad de la onda en
este caso viene dado por u = ? k 2 m (13) Por lo tanto la velocidad de las
ondas de la materia no es constante como la de las ondas de radiación,
pero es un función del número de onda k. la ecuación (12)
podría ser reorganizado como - h 2 2 m (Ik) 2 = I ? (- i ?) Multiplicando
ambos lados por ?, a la vez que podemos ver a partir de las ecuaciones (8) y (
9) que - H 2 2 m ? 2 ? ? x 2 = I ? ? ? ? t (14) que es la ecuación que
rige para la onda asociada a la partícula libre que estamos buscando.
Esta es la ecuación de Schrödinger para la partícula libre. Es
la ecuación en la región de tiempo que corresponde a la primera ley
de la región del espacio-tiempo de Newton. Con el fin de incluir las
interacciones de las partículas con el medio ambiente se observa que la
energía total del como una partícula se compone de la energía
cinética y la energía potencial. Este último podría ser
tomado como sólo depende de la posición y representado por una
función de energía potencial V (x). Así, para un conservador
sistema que tenemos la energía constante E total dado por
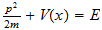
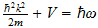
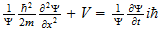
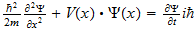
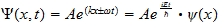
Página 5
p 2 2 m + V (x) = E (15) La relación con el número de frecuencias de
onda correspondiente, asociando frecuencia con la energía total, es ? 2 k
2 2 m + V = ? ? Ecuaciones Adopción (8) y ( 9) , como antes, llegamos a
la ecuación de onda de Schrödinger con la interacción presentar
- h 2 2 m ? 2 ? ? x 2 + V (x) =
 ? i ? ? ? ? t (16) Esto corresponde en la región tiempo para la segunda
ley de Newton en la región del espacio-tiempo. Como puede verse a partir
de las derivaciones anteriores, nada en contra de los principios de la Sistema
recíproco se ha introducido hasta el momento. Por lo tanto las ecuaciones
de Schrödinger pueden ser admitidos como gobernante legítimo
principios para llegar a las posibles funciones de onda de una partícula
hipotética de la masa m de desplazamiento la región de tiempo, con o
sin funciones potenciales de energía como puede ser el caso. Podemos
observar en el paso, que a menudo una considerable destreza matemática se
requiere en la solución de estos diferencial ecuaciones, aunque los
métodos numéricos para computador están rápidamente
reemplazando a las soluciones de forma cerrada. Cualquiera de onda
correspondiente a un estado de energía definida E tiene una frecuencia ?
definida = e / h. Por lo tanto partir de la ecuación (7) se puede
escribir ? (x, t) = A
? i ? ? ? ? t (16) Esto corresponde en la región tiempo para la segunda
ley de Newton en la región del espacio-tiempo. Como puede verse a partir
de las derivaciones anteriores, nada en contra de los principios de la Sistema
recíproco se ha introducido hasta el momento. Por lo tanto las ecuaciones
de Schrödinger pueden ser admitidos como gobernante legítimo
principios para llegar a las posibles funciones de onda de una partícula
hipotética de la masa m de desplazamiento la región de tiempo, con o
sin funciones potenciales de energía como puede ser el caso. Podemos
observar en el paso, que a menudo una considerable destreza matemática se
requiere en la solución de estos diferencial ecuaciones, aunque los
métodos numéricos para computador están rápidamente
reemplazando a las soluciones de forma cerrada. Cualquiera de onda
correspondiente a un estado de energía definida E tiene una frecuencia ?
definida = e / h. Por lo tanto partir de la ecuación (7) se puede
escribir ? (x, t) = A
 correo - I E t ?
correo - I E t ?
 ? (x) (17) donde ? (x) es una función de la única variable espacio.
Inserción de lo anterior en la ecuación (16) y dividiendo a cabo el
factor de correo -IET / h todo, se obtiene la ecuación diferencial que
deben cumplir ? (x) - h 2 2m ? 2 ? ? x 2 + V (x)
? (x) (17) donde ? (x) es una función de la única variable espacio.
Inserción de lo anterior en la ecuación (16) y dividiendo a cabo el
factor de correo -IET / h todo, se obtiene la ecuación diferencial que
deben cumplir ? (x) - h 2 2m ? 2 ? ? x 2 + V (x)
 ? (x) = E
? (x) = E
 ? (x) (18) que se conoce como la ecuación de Schrödinger
independiente del tiempo. Esta ecuación es menos general y es válida
sólo para los estados de energía total definitivo.
? (x) (18) que se conoce como la ecuación de Schrödinger
independiente del tiempo. Esta ecuación es menos general y es válida
sólo para los estados de energía total definitivo.
3 estados de energía negativa
Es interesante ver lo que las
soluciones de la ecuación de Schrödinger llegar a ser. En primer
lugar, en cualquier región de constante de energía potencial V,
vemos que la solución de la ecuación (18) es una función
sinusoidal, ? (x) = A
 sen (kx) o A
sen (kx) o A
 cos (kx) k 2 = 2 m
cos (kx) k 2 = 2 m
 (E - V) ? 2 } (19) (E - V) es la energía cinética.
(E - V) ? 2 } (19) (E - V) es la energía cinética.
Página 6
3.1 La Función De Figura 1: Energía Potencial Paso En la Figura 1 (
a) nos imaginamos una energía potencial paso a función, que es
constante en V 1 y V 2 , respectivamente, en dos regiones diferentes. Una
posible función de onda correspondiente a este caso se muestra en la
Figura 1 (b). La mayor energía cinética de la partícula (E - V
1 ) En la región x <0 se refleja en el número de onda más
grande (Longitud de onda más pequeña) en esta región. Asimismo,
puesto que su velocidad en esta región es mayor, lo que gasta
comparativamente menos tiempo en esta región, y esto se refleja como su
amplitud más pequeña en esta región. Un caso interesante se
produce cuando la energía potencial V en cualquier región es mayor
que la energía total E. Aquí la energía cinética, E - V,
se convierte en negativo Es físicamente imposible en la región del
espacio-tiempo! y la partícula no puede entrar en esa región. Sin
embargo, la situación es diferente en la región de tiempo: La
ecuación ( 18) tiene soluciones válidas en la región, con k de
la ecuación ( 19) teniendo en valores imaginarios, ? (x) = A
 e \ bx b = i
e \ bx b = i
 k } (20) El signo del exponente se elige de tal manera como para ver que ?
tiende a cero para x grande. Figura 2 ilustra este caso: en la región
x> 0 vemos que E es menor que la energía potencial. La función de
onda es sinusoidal en la región de la energía cinética positiva
y es exponencial en la región de la energía cinética negativa.
Ambos funciones unirse sin problemas en x = 0 con una primera orden de
continuidad. La penetración de la función de onda en la región
de la energía cinética negativa no tiene analógica clásica
y es puramente un fenómeno de las veces región. 0 x ? (x) (B) V 1 V
2 V (x) E 0 x (A) E - V 1
k } (20) El signo del exponente se elige de tal manera como para ver que ?
tiende a cero para x grande. Figura 2 ilustra este caso: en la región
x> 0 vemos que E es menor que la energía potencial. La función de
onda es sinusoidal en la región de la energía cinética positiva
y es exponencial en la región de la energía cinética negativa.
Ambos funciones unirse sin problemas en x = 0 con una primera orden de
continuidad. La penetración de la función de onda en la región
de la energía cinética negativa no tiene analógica clásica
y es puramente un fenómeno de las veces región. 0 x ? (x) (B) V 1 V
2 V (x) E 0 x (A) E - V 1
Page 7
Quantum Mechanics 7 Figura 2: La energía cinética negativa
3.2 Explicación de los estados de energía negativa
Cuando nos dirigimos al Sistema
Recíproca para obtener una explicación de la posibilidad de la
existencia de estados de energía negativa, lo que encontramos es el
siguiente. En la región de espacio-tiempo, es decir, en el contexto de la
sistema de referencia espacial tridimensional, velocidad (espacio / tiempo) es
vectorial, es decir, puede tener sentido en espacio, por lo que podría
tomar valores positivos o negativos. Esto es porque en este caso el espacio es
tridimensional y el tiempo es escalar. En este marco, la energía, la cual
es la velocidad inversa unidimensional (Tiempo / espacio), es escalar, y puede
tomar únicamente en valores de cero o positivo. Por otra parte, la
región de tiempo es un dominio de la trama de referencia temporal en tres
dimensiones. En este caso el tiempo es de tres dimensiones y el espacio es
escalar. Por consiguiente, la velocidad inversa (es decir, la energía) es
la cantidad que es ''Direccional'', es decir, puede tomar una ''dirección
temporal'' en el contexto de las tres dimensiones marco de referencia
temporal. Por lo tanto, es perfectamente posible para que tome en valores
negativos también. (Se debe ser advertido de que ''la dirección en
el tiempo'' no tiene nada que ver con la dirección en el espacio, sino
que ha de ser entendimos que sólo estamos hablando metafóricamente.)
Además, en la región de tiempo, la velocidad es la cantidad que es
escalar, siendo un ejemplo la velocidad de desplazamiento total neto del
átomo, a saber, la atómica número Z. Por otra parte la
posibilidad de que incluso la energía potencial (siendo una velocidad
inversa) podría ser ''direccional'' en el tiempo en tres dimensiones, y
por lo tanto estar representado por números complejos en la región
de tiempo, no puede pasarse por alto. De hecho, los teóricos
cuánticos resulta necesario adoptar el complejo potencial
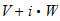 en lugar de la
en lugar de la
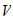 en la teoría de la dispersión. Aquí el número de onda
en la teoría de la dispersión. Aquí el número de onda
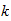 se vuelve compleja y se escribe como
se vuelve compleja y se escribe como
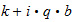 de La ecuación (20) se convierte en
de La ecuación (20) se convierte en
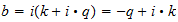 ,
y tenemos
,
y tenemos
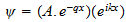 (21) Al
mismo tiempo podemos ver que se trata de la función de onda de una onda
de cuya amplitud disminuye a medida que avances, y por lo tanto representa un
haz de partículas algunas de las cuales están siendo absorbidos.
(21) Al
mismo tiempo podemos ver que se trata de la función de onda de una onda
de cuya amplitud disminuye a medida que avances, y por lo tanto representa un
haz de partículas algunas de las cuales están siendo absorbidos.
3.2Explanation of the Negative Energy States
When we turn to the Reciprocal System for an explanation of the possibility of the existence of negative energy states, what we find is as follows. In the time-space region, that is, in the context of the three-dimensional spatial reference frame, speed (space/time) is vectorial, that is, can have direction in space and therefore could take on positive or negative values. This is because in this case space is three-dimensional and time is scalar. In this frame, energy, which is one-dimensional inverse speed (time/space), is scalar, and can take on zero or positive values only. On the other hand, the time region is a domain of the three-dimensional temporal reference frame. In this case time is three-dimensional and space is scalar. Consequently the inverse speed (namely, energy) is the quantity that is directional, that is, can take on a temporal direction in the context of the three-dimensional temporal reference frame. Therefore it is perfectly possible for it to take on negative values as well. (It must be cautioned that direction in time has nothing to do with direction in space; it is to be understood that we are only speaking metaphorically.) Further, in the time region, speed is the quantity that is scalar, an example being the net total speed displacement of the atom, namely, the atomic number Z.
Moreover the possibility that even potential energy (being an inverse speed)
could be directional in the three-dimensional time, and hence be represented
by complex numbers in the time region, cannot be overlooked. Indeed the
Quantum theorists find it necessary to adopt the complex potential
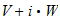 in place of
in place of
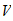 in scattering theory. Here the wave number
in scattering theory. Here the wave number
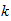 becomes complex and is written as
becomes complex and is written as
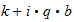 of Equation (20) becomes
of Equation (20) becomes
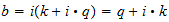 ,
and we have
,
and we have
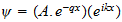 (21)
(21)
We can at once see that this is the wave function of a traveling wave of whose amplitude decreases as it advances, and therefore represents a beam of particles some of which are getting absorbed.
Página 8
8 Quantum Mechanics 3.3 La barrera de energía potencial Figura 3: Potencial Barrera de Energía Una situación interesante surge cuando dos regiones de la energía cinética positivos ocurren separados por una barrera de energía potencial que es mayor que la energía total como se muestra en F igura 3 ( a). En el centro de región (de la energía cinética negativa) la función de onda es exponencial, mientras que es sinusoidal a cada lado como se muestra en F igura 3 ( b). En cualquier límite de la función y su primera derivada son continuas. De esto es evidente que la partícula representado por la onda tiene una probabilidad no cero de que aparece en el otro lado de la barrera! Mientras que esto es una región fenómeno en tiempo real que se ha observado (el ''Túnel''), que no tiene ningún análogo en la región de espacio-tiempo (mecánica clásica). 3.4 El pozo de energía potencial Figura 4: Energía potencial Bueno 0 x ? (x) (B) V 1 V (x) E 0 x (A) -L L 0 x ? (x) (B) V 1 V (x) E 0 x (A) -L L
Página 9
Quantum Mechanics 9 El último caso de interés queremos considerar es
la de un potencial ell w como se muestra en la Figura 4 (a), en el que la
energía total E es menor que la energía potencial V 1 en las
regiones exteriores. Al igual que antes, nos encontramos con que el
función de onda es sinusoidal en la región (central) de la
energía cinética positiva, y es exponencial en el (Exterior)
regiones de energía cinética negativa, manteniendo la continuidad
primera orden en las fronteras. Pero aquí un nuevo factor que emerge, a
saber, que si elegimos un valor arbitrario de E, podría ser necesario
adoptar crecimiento exponenciales en las regiones exteriores (por ejemplo,
correo + Bx para x> L) con el fin de satisfacer la condiciones de
continuidad en la frontera. Por tanto, esto nos lleva a un estado irreal de
las cosas. La física requisito es que la función de onda va hacia
cero con el aumento de espacio de coordenadas en el exterior regiones. Esto
requiere la elección de exponenciales disminución en las regiones
exteriores (por ejemplo, correo -Bx para x> L). Este requisito, junto con
las restricciones de continuidad en el límite, limita la posible
energías a una serie de niveles diferentes, cada uno con su propia
función de onda. Por lo tanto, la energía potencial de tipo así
funciones dan lugar a un conjunto de posibles niveles de energía
discretos. Este hecho se puede ver directamente a llevar a la explicación
de varios hechos observables incluyendo los espectros atómica. 4 Origen
del principio de exclusión de Pauli El llamado principio de
exclusión fue promulgada originalmente por Wolfgang Pauli. Esta es
empírico ley a la que se ha encontrado una excepción. Ha sido un
principio rector heurística para entender muchos un fenómeno
cuántico importante. A pesar de su importante papel, la explicación
de su origen tiene desafiado a los teóricos. Por lo tanto, que esta
explicación es ahora inminente del sistema Recíproca es una punto a
favor de la naturaleza general de esta última teoría. 4.1 La Vuelta
Pero primero hay que reconocer un punto que hemos estado haciendo
hincapié, 3 , 4 a saber, que el espacio de rotación es tan
fundamentales como el espacio lineal (extensión). Larson explica: ''...
el electrón es esencialmente nada más de una unidad de rotación
de espacio. Este es un concepto que es bastante difícil para la
mayoría de nosotros cuando se trata primero encontró, porque entra
en conflicto con la idea de la naturaleza del espacio que hemos obtenido a
partir de un largo continuo, pero no crítica, el examen de lo que nos
rodea. ... El descubrimiento de que el ''espacio'' de nuestra la experiencia
ordinaria, el espacio de extensión, ya que estamos pidiendo en este
trabajo, no es más que una manifestación de espacio, en general, se
abre la puerta a la comprensión de muchos aspectos del universo
físico ... '' 5 Él señala que un átomo, por ejemplo, puede
existir en una unidad de espacio de giro, ya que puede en una unidad de
espacio de extensión. En un documento titulado ''Photon como Birotation''
6 hemos deducido que la unidad básica del momento angular es
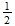 h. Ahora nos encontramos con que los teóricos cuánticos se han
referido a esta unidad básica del espacio de rotación como el giro.
Además de las tres coordenadas del espacio, giro se trata como un cuarto
de coordenadas. Por lo tanto dos diferentes partículas pueden ocupar el
mismo lugar en el espacio de extensión en el mismo tiempo si su giro
difiere de coordenadas. 4.2 Indistinguibilidad En relación con una clase
de partículas elementales, sabemos que dos partículas individuales
(por ejemplo, dos electrones) son absolutamente iguales. En la región del
espacio-tiempo, el hecho de que dos partículas están presentes
idénticos 3 KVK Nehru, '' La Ley de Conservación de la
Dirección , ''Reciprocidad, vol. XVIII, ? 3, otoño 1989, p. 3. 4 KVK
Nehru, '' Sobre la naturaleza de la rotación y Birotation ,
''Reciprocidad, vol. XX, ? 1, Spring 1991, p. 8. 5 Larson DB, materia y sus
propiedades , La Sociedad Internacional de la Ciencia Unificada, Utah, EE.UU.,
1988, pp 102-3. 6 KVK Nehru, '' El Photon como Birotation , ''Reciprocidad,
vol. XXV, ? 3, invierno 1996/97, pp 11-16
h. Ahora nos encontramos con que los teóricos cuánticos se han
referido a esta unidad básica del espacio de rotación como el giro.
Además de las tres coordenadas del espacio, giro se trata como un cuarto
de coordenadas. Por lo tanto dos diferentes partículas pueden ocupar el
mismo lugar en el espacio de extensión en el mismo tiempo si su giro
difiere de coordenadas. 4.2 Indistinguibilidad En relación con una clase
de partículas elementales, sabemos que dos partículas individuales
(por ejemplo, dos electrones) son absolutamente iguales. En la región del
espacio-tiempo, el hecho de que dos partículas están presentes
idénticos 3 KVK Nehru, '' La Ley de Conservación de la
Dirección , ''Reciprocidad, vol. XVIII, ? 3, otoño 1989, p. 3. 4 KVK
Nehru, '' Sobre la naturaleza de la rotación y Birotation ,
''Reciprocidad, vol. XX, ? 1, Spring 1991, p. 8. 5 Larson DB, materia y sus
propiedades , La Sociedad Internacional de la Ciencia Unificada, Utah, EE.UU.,
1988, pp 102-3. 6 KVK Nehru, '' El Photon como Birotation , ''Reciprocidad,
vol. XXV, ? 3, invierno 1996/97, pp 11-16
Página 10
10 Quantum Mechanics sin complicaciones ya que se pueden mantener distingue
por sus respectivas ubicaciones. Pero en la cuántica fenómenos,
debido a la naturaleza no local de la región de tiempo, tal
distinción no es posible. Este indistinguishability intrínseca da
lugar a algunas restricciones especiales. Tomemos ? (1,2) que la onda
función de dos partículas indistinguibles con la partícula 1 en
la posición r 1 (Cuyas coordenadas incluir la girar coordinar
también) y la partícula 2 en la posición r 2 . Entonces [?
(1,2)] 2 representa la distribución de probabilidad para la
partícula 1 a estar en r 1 y partículas 2 para estar en r 2 . Ya que
no podemos distinguir entre las partículas, función de onda debe ser
de una forma tal que da lugar a la misma distribución de probabilidad si
se intercambiar las dos partículas en ?. Es decir [? (1,2)] 2 = [?
(2,1)] 2 Esto puede ser satisfecha de dos maneras, ? (1,2) = + ? (2,1) ? (1,2)
=-? (2,1) } (22) El primer tipo de funciones de onda se conoce como la
simétrica y la segunda como la antisimétrica funciones. Ahora el
hallazgo empírico es que las funciones de onda de las partículas
como los protones y los neutrones que son sabe que tienen espín
media-integral
(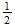 h) ¿antisimétrica, y las de partículas con spin entero (Como
los fotones) son simétricos. La afirmación más fundamental de
principio de exclusión de Pauli se algo así como esto: ''Cualquier
función de onda permite que un sistema de partículas spin-media debe
ser antisimétrica con respecto al intercambio de todas las coordenadas
(espacio y giro) de cualquier par de partículas ''. Pero enunciar un
principio es muy diferente de explicar su origen, y el hecho es que no
explicación teórica se ha encontrado para este hallazgo
empírico. Un autor escribe: ''Por razones que no se entiende claramente,
para los electrones, protones, neutrones, y todas las demás
partículas spin
h) ¿antisimétrica, y las de partículas con spin entero (Como
los fotones) son simétricos. La afirmación más fundamental de
principio de exclusión de Pauli se algo así como esto: ''Cualquier
función de onda permite que un sistema de partículas spin-media debe
ser antisimétrica con respecto al intercambio de todas las coordenadas
(espacio y giro) de cualquier par de partículas ''. Pero enunciar un
principio es muy diferente de explicar su origen, y el hecho es que no
explicación teórica se ha encontrado para este hallazgo
empírico. Un autor escribe: ''Por razones que no se entiende claramente,
para los electrones, protones, neutrones, y todas las demás
partículas spin
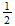 ,
el menos signo se elige ... '' 7 4.3 Los dos tipos de puntos de referencia
Desde el sistema recíproco que tenemos ahora la explicación.
Recordemos que en el universo de movimiento hay dos tipos de marcos de
referencia-el convencional, estacionario en tres dimensiones espaciales marco
de referencia (o su análogo cósmica, el marco de referencia temporal
de tres dimensiones) y el movimiento marco de referencia natural. También
tenemos dos tipos de objetos, los que tienen movimiento independiente como la
partículas que gravitan y aquellos que no tienen movimiento independiente
de su propia y por lo tanto son estacionarias en el marco de referencia
natural, como los fotones y las partículas que tienen masa potencial 8
sólo. La punto de referencia para el escalar movimiento hacia adentro de
la partícula gravitante es la propia partícula. Por lo tanto si hay
son dos lugares A y B en el marco de referencia de tres dimensiones con esta
partícula situada en A, por ejemplo, sus movimientos gravitacionales
aparece en la dirección BA, porque es hacia el interior, hacia sí
mismo. Si ahora la partícula se desplaza a la posición B, la
dirección de su movimiento gravitatorio parece invertirse, siendo en el
AB dirección. Este es el origen de la antisimetría de las funciones
de onda de tales partículas. Como ya se ha señalado, una unidad de
rotación unidimensional lleva unidad de giro
(
,
el menos signo se elige ... '' 7 4.3 Los dos tipos de puntos de referencia
Desde el sistema recíproco que tenemos ahora la explicación.
Recordemos que en el universo de movimiento hay dos tipos de marcos de
referencia-el convencional, estacionario en tres dimensiones espaciales marco
de referencia (o su análogo cósmica, el marco de referencia temporal
de tres dimensiones) y el movimiento marco de referencia natural. También
tenemos dos tipos de objetos, los que tienen movimiento independiente como la
partículas que gravitan y aquellos que no tienen movimiento independiente
de su propia y por lo tanto son estacionarias en el marco de referencia
natural, como los fotones y las partículas que tienen masa potencial 8
sólo. La punto de referencia para el escalar movimiento hacia adentro de
la partícula gravitante es la propia partícula. Por lo tanto si hay
son dos lugares A y B en el marco de referencia de tres dimensiones con esta
partícula situada en A, por ejemplo, sus movimientos gravitacionales
aparece en la dirección BA, porque es hacia el interior, hacia sí
mismo. Si ahora la partícula se desplaza a la posición B, la
dirección de su movimiento gravitatorio parece invertirse, siendo en el
AB dirección. Este es el origen de la antisimetría de las funciones
de onda de tales partículas. Como ya se ha señalado, una unidad de
rotación unidimensional lleva unidad de giro
(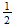 hora). El giro resultante de un rotación de dos dimensiones con la unidad
de giro en cada dimensión es 1 \ 1 = 1 (es decir,
hora). El giro resultante de un rotación de dos dimensiones con la unidad
de giro en cada dimensión es 1 \ 1 = 1 (es decir,
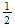 H) o es 1 \ (-1) = -1 (que Es decir, -
H) o es 1 \ (-1) = -1 (que Es decir, -
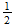 horas). Por otra parte, el giro resultante de un birotation (como el
fotón) es 1 1 = 2 (es decir, H) o 1-1 = 0. Desde la gravitación
surge de la rotación de dos dimensiones, podemos ver que una gravitante
partícula lleva
spin-
horas). Por otra parte, el giro resultante de un birotation (como el
fotón) es 1 1 = 2 (es decir, H) o 1-1 = 0. Desde la gravitación
surge de la rotación de dos dimensiones, podemos ver que una gravitante
partícula lleva
spin-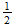 .
Por lo tanto la función de onda de las partículas de espín
.
Por lo tanto la función de onda de las partículas de espín
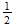 -resulta
ser antisimétrica. 7 Cohen, BL, Conceptos de Física Nuclear, Tata
McGraw Hill, India, 1971, p. 38. 8 Larson DB, nada más que de movimiento,
North Publishers Pacífico, Oregon, EE.UU., 1979, pp 141-2 , 165-7 .
-resulta
ser antisimétrica. 7 Cohen, BL, Conceptos de Física Nuclear, Tata
McGraw Hill, India, 1971, p. 38. 8 Larson DB, nada más que de movimiento,
North Publishers Pacífico, Oregon, EE.UU., 1979, pp 141-2 , 165-7 .
Página 11
Quantum Mechanics 11 Por otra parte, el punto de referencia para el movimiento de las partículas como los fotones es la ubicación en la marco de referencia natural, o lo que Larson llama a la ''posición absoluta.'' El marco de referencia natural es no es un distribuidor espacial, ni es un colector temporal. Es un colector de velocidad: cada lugar en que es que se mueve a velocidad de la unidad, una unidad de espacio por unidad de tiempo. Supongamos que la separación espacial entre dos lugares en este marco (las ubicaciones absolutas) aumenta en unidades naturales n del espacio. Debido a la criterio de velocidad de la unidad, hay un aumento concomitante en la separación en el tiempo por n unidades naturales de tiempo, haciendo n / n = 1. La expansión en el espacio está completamente anulada por la expansión en el tiempo (ya que un aumentar en el espacio es equivalente a una disminución en el tiempo y viceversa), y desde un punto de espacio-tiempo ver que no hay separación entre los lugares absolutos. En el contexto de la trama de referencia tridimensional, los fotones parecen moverse hacia fuera desde el punto de origen. Pero ya hemos visto que el fotón está parado en la ubicación absoluta. Su movimiento aparente es el movimiento hacia el exterior de la ubicación absoluta (en la que se encuentra) lejos de todo otros lugares absolutos. El punto crucial que debe ser reconocida ahora es que hacia el exterior de una ubicación absoluta sigue siendo hacia fuera desde cualquier otra ubicación absoluta debido a la equivalencia de estos ubicaciones absolutas como se explicó anteriormente. Por lo tanto, intercambiando la ubicación del fotón entre dos tales ubicaciones absolutas no tiene ningún efecto sobre la señal de su función de onda. Es decir, la función de onda de tales partículas es simétrica. Una palabra final es el fin: todo lo que se ha dicho anteriormente, también es cierto en el tiempo región, excepto que la dirección escalar hacia el exterior en la región de espacio-tiempo se manifiesta como hacia el interior en el momento región y viceversa. 5 Potenciales en la región de tiempo Por último, podría ser de interés para explorar la naturaleza y el tipo de las funciones de energía potencial V (véase La ecuación ( 15)) , en la región de tiempo. En vista de la naturaleza de soltera de la investigación y la insuficiente tiempo disponible, los resultados presentados en esta sección puede tener que ser tratada como provisional. 5.1 Las relaciones dimensionales entre las regiones Discutir el efecto de la inversión de tiempo y espacio a nivel de unidad de las dimensiones de inter- las relaciones regionales, Larson 9 muestra que las expresiones para la velocidad y las cantidades relacionadas con la velocidad en el región de tiempo son los segundos expresiones de energía de las cantidades correspondientes que pertenecen a la vez- región de espacio. Esto es porque el movimiento (velocidad) tiene un componente espacial y un componente temporal. Desde espacio de unidad es lo mínimo que puede existir, en el plazo de región la región dentro de la unidad espacio-el componente espacial de una velocidad permanece constante a 1 unidad y toda la variabilidad puede ser en lo temporal componente, t, sólo. En virtud de la relación recíproca entre el espacio y el tiempo de los t unidades de tiempo son equivalente a 1 unidad / t de espacio y se manifiestan por lo que en la región de tiempo. Es por eso que Larson se utiliza el término espacio equivalente (es decir, el espacio inversa) como sinónimo de región de tiempo. La velocidad equivalente en el momento región es, por lo tanto, determinada por la proporción entre el espacio equivalente a tiempo, (1 / t) / t = 1 / t 2 . Esta cantidad es la segunda expresión de potencia de la velocidad en la región de tiempo-espacio con 1 unidad de componente espacial y t unidades de componente de tiempo, a saber, 1 / t. En un artículo anterior 1 hemos identificado dos zonas diferentes de la región de tiempo, a saber, el de una sola dimensional y las tres dimensiones. La segunda relación de poder se ha mencionado anteriormente se podía ver a se aplican específicamente a la zona unidimensional, la zona de rotación de una dimensión asociada con los átomos o subatoms. Por otro lado, para la zona en tres dimensiones-donde el compuesto 9 Ibid., p. 155 .
Página 12
12 Quantum Mechanics movimientos que constituyen un átomo de existir-la
situación es diferente porque el giro básico que constituye el
átomo es de dos dimensiones. El componente temporal de una rotación
de dos dimensiones en la región de tiempo sería t 2 , Y su
equivalente espacial es 1 / t 2 . Así que la velocidad equivalente en el
caso de dos dimensiones rotación resulta ser (1 / t 2 ) / T 2 = 1 / t 4 .
Como puede verse, esta es la cuarta potencia de la expresión
correspondiente espacio-región de velocidad 1 / t. (Tenga en cuenta que
en el momento región de espacio-tiempo es escalar y hay No puede ser
cualquier cosa como el tiempo de dos dimensiones.) Mirando hacia atrás,
podemos ver fácilmente por qué los teóricos cuánticos
requieren números complejos para hacer frente con los llamados ''niveles
de energía electrónica'' del átomo de forma adecuada: que
tenían que hacer frente con la carácter bidimensional de la
velocidad relativa equivalente a la rotación de una dimensión en el
tiempo región. También se sugiere que se requiere la adopción
de cuaterniones para manejar la llamada ''nuclear los niveles de energía
'', ya que la dimensionalidad de la velocidad equivalente pertenecientes a las
dos dimensiones la rotación en la región de tiempo es de cuatro. 5.2
Potenciales de la región espacio-temporal En esta etapa de nuestro
estudio tenemos sólo dos movimientos escalares (fuerzas) a tener en
cuenta: el espacio-tiempo la progresión y la gravitación. En la zona
exterior (la región del espacio-tiempo), la Fuerza Pública por el
espacio- tiempo de progresión y la gravedad se recogen, respectivamente,
por F Correos = K Correos F GO = - K GO r 2 } (23) donde todas las cantidades
en cuestión son las unidades naturales, la K 's son constantes positivas
y la r factor de distancia. Sufijo G se refiere a la gravedad, P a la
progresión del espacio-tiempo y la O a la región exterior. De la
definición de potencial, F = - ? V / ? r, obtenemos las expresiones para
los potenciales correspondientes debido a la progresión de espacio-tiempo
y la gravitación, en la región exterior, respectivamente, como V
Correos = - K Correos
 r V GO = - K GO r } (24) El potencial debido a la evolución
espacio-tiempo es repulsivo, mientras que, debido a la gravedad es atractiva
como puede ser visto. 5.3 Potenciales en la Zona Uno-dimensional de la
región de tiempo La energía potencial de ser velocidad inversa, las
expresiones para los potenciales en la zona de una dimensión de la
región de tiempo sería el segundo expresiones de poder de los
correspondientes en el tiempo-espacio región (Sección 5.1 ). Por
consiguiente, la progresión de espacio-tiempo y los potenciales
gravitacionales en esta zona puede ser escrito como V P1 = K P1
r V GO = - K GO r } (24) El potencial debido a la evolución
espacio-tiempo es repulsivo, mientras que, debido a la gravedad es atractiva
como puede ser visto. 5.3 Potenciales en la Zona Uno-dimensional de la
región de tiempo La energía potencial de ser velocidad inversa, las
expresiones para los potenciales en la zona de una dimensión de la
región de tiempo sería el segundo expresiones de poder de los
correspondientes en el tiempo-espacio región (Sección 5.1 ). Por
consiguiente, la progresión de espacio-tiempo y los potenciales
gravitacionales en esta zona puede ser escrito como V P1 = K P1
 r 2 V G1 = K G1 r 2 } (25) con el sufijo 1 se refiere a la zona de una sola
dimensión. Podemos a la vez comprobar que la gravedad es repulsiva
r 2 V G1 = K G1 r 2 } (25) con el sufijo 1 se refiere a la zona de una sola
dimensión. Podemos a la vez comprobar que la gravedad es repulsiva
Página 13
Quantum Mechanics 13 y la progresión espacio-tiempo atractivo en esta
región. Además podría ser un término constante K I1 , que
representa el nivel inicial de la potencial región de tiempo. Así,
el tiempo total de la región potencial en el que- zona dimensiones
resulta ser V T1 = K P1
 r 2 + K G1 r 2 \ K I1 (26) Los valores de K G1 y K I1 , Y, posiblemente, K P1
, Son funciones de los desplazamientos del átomo en los tres dimensiones
escalares. Es interesante ver lo que las expresiones de las fuerzas
correspondientes serían: la diferenciación con con respecto a r y
tomando el signo negativo, tenemos F P1 = -2
r 2 + K G1 r 2 \ K I1 (26) Los valores de K G1 y K I1 , Y, posiblemente, K P1
, Son funciones de los desplazamientos del átomo en los tres dimensiones
escalares. Es interesante ver lo que las expresiones de las fuerzas
correspondientes serían: la diferenciación con con respecto a r y
tomando el signo negativo, tenemos F P1 = -2
 K P1
K P1
 r F G1 = 2
r F G1 = 2
 K G1 r 3 } (27) Larson 10 Sin embargo, al calcular las distancias
interatómicas en los sólidos, basándose en el equilibrio de las
fuerzas de zonas horarias, adopta F P1 = -1 F G1 = K r 4 } (28) donde K es una
función de las varias rotaciones atómicas. Estas expresiones se
pueden ver a diferir de Las ecuaciones (27) por encima. Pero si tomamos las
ecuaciones (27) o las ecuaciones ( 28), el equilibrio de la fuerza
ecuación, F P1 F = G1 se puede observar que conduzca a la misma
dependencia de energía cuarto en el factor de distancia. Por lo tanto,
incluso si nos encontramos con que las ecuaciones (27) son adoptadas con
preferencia a las ecuaciones (28), Cálculos de distancia
inter-atómicas originales de Larson permanecerían inalteradas. La
región de tiempo ecuación del potencial ( 26) resulta en un pozo de
potencial y por lo tanto las soluciones de La ecuación de
Schrödinger ( 18) producen un conjunto de niveles discretos de
energía para el sistema atómico (véase la sección 3.4 ).
Queda por comprobado si realmente estos corresponden a los valores inferidos a
partir de la datos espectroscópicos. 5.4 Potenciales en la zona
tridimensional de la región de tiempo Volviendo ahora a los potenciales
en la zona de tres dimensiones, siguiendo nuestro análisis anterior de la
situación dimensional (Sección 5. 1), que adopte las expresiones
cuarta potencia de la correspondiente fuera de la región cantidades (es
decir, la región de espacio-tiempo) de las Ecs. (24) V P3 = K P3
K G1 r 3 } (27) Larson 10 Sin embargo, al calcular las distancias
interatómicas en los sólidos, basándose en el equilibrio de las
fuerzas de zonas horarias, adopta F P1 = -1 F G1 = K r 4 } (28) donde K es una
función de las varias rotaciones atómicas. Estas expresiones se
pueden ver a diferir de Las ecuaciones (27) por encima. Pero si tomamos las
ecuaciones (27) o las ecuaciones ( 28), el equilibrio de la fuerza
ecuación, F P1 F = G1 se puede observar que conduzca a la misma
dependencia de energía cuarto en el factor de distancia. Por lo tanto,
incluso si nos encontramos con que las ecuaciones (27) son adoptadas con
preferencia a las ecuaciones (28), Cálculos de distancia
inter-atómicas originales de Larson permanecerían inalteradas. La
región de tiempo ecuación del potencial ( 26) resulta en un pozo de
potencial y por lo tanto las soluciones de La ecuación de
Schrödinger ( 18) producen un conjunto de niveles discretos de
energía para el sistema atómico (véase la sección 3.4 ).
Queda por comprobado si realmente estos corresponden a los valores inferidos a
partir de la datos espectroscópicos. 5.4 Potenciales en la zona
tridimensional de la región de tiempo Volviendo ahora a los potenciales
en la zona de tres dimensiones, siguiendo nuestro análisis anterior de la
situación dimensional (Sección 5. 1), que adopte las expresiones
cuarta potencia de la correspondiente fuera de la región cantidades (es
decir, la región de espacio-tiempo) de las Ecs. (24) V P3 = K P3
 r 4 V G3 = K G3 r 4 } (29) 3 con el sufijo que denota la zona tridimensional.
Sabemos que la evolución espacio-tiempo actúa fuera de la unidad de
espacio. En la región del espacio-tiempo de distancia 10 Larson, Dewey
B., materia y sus propiedades, op. cit., p. 8 .
r 4 V G3 = K G3 r 4 } (29) 3 con el sufijo que denota la zona tridimensional.
Sabemos que la evolución espacio-tiempo actúa fuera de la unidad de
espacio. En la región del espacio-tiempo de distancia 10 Larson, Dewey
B., materia y sus propiedades, op. cit., p. 8 .
Página 14
14 Quantum Mechanics de la unidad es también lejos de cero (el origen del
sistema de referencia espacial convencional), mientras que en el región
de tiempo (es decir, en menos de espacio de unidad) de distancia de la unidad
es hacia cero. Esta es la razón por la la progresión de
espacio-tiempo es un movimiento hacia el exterior en la región exterior,
mientras que es hacia el interior en la región de tiempo. Esto es cierto
en la zona de una dimensión de la región de tiempo tanto como en la
zona de tres dimensiones. Sin embargo, la ''unidad'' de la zona tridimensional
no coincide con la ''unidad'' de la unidimensional zona. Su límite se
determina por el tamaño aparente del átomo en cuestión. Esto es
debido a que el átomo y la zona de tres dimensiones son una y la misma
cosa. (Debemos evitar caer en la trampa de imaginando que primero hay un
átomo, y que ''ocupa'' la zona tridimensional pre-existente!) En La
ecuación (7) del artículo sobre la mecánica ondulatoria 1 hemos
derivado la siguiente expresión para el tamaño del átomo, r La
= 1,2 \ A Tercera femtometers donde A es el peso atómico. Expresando esto
en las unidades naturales como r Un , Ahora observamos que la referencia punto
de distancia cómputo en el caso de V P3 no es el origen del sistema de
referencia, pero el punto en el r Un . Por último, ya que el potencial
debido a la progresión tiene que ser atractivo un signo menos tiene que
ser introducido. Por lo tanto las expresiones para los dos potenciales
están V P3 = - K P3
 (r Un - R) 4 V G3 = K G3 t 4 } (30) Adición de un término constante
K I3 para cuidar de nivel inicial de la energía potencial, tenemos el
total de expresión para el potencial de la zona tridimensional de la
región de tiempo como V T3 = - K P3
(r Un - R) 4 V G3 = K G3 t 4 } (30) Adición de un término constante
K I3 para cuidar de nivel inicial de la energía potencial, tenemos el
total de expresión para el potencial de la zona tridimensional de la
región de tiempo como V T3 = - K P3
 (r Un
(r Un
 r) 4 + K G3 r 4 \ K I3 (31) Tomamos nota de que esto corresponde a lo que los
teóricos cuánticos convencionales llamarían la nuclear
potencial. Nuestro estudio indica que la ecuación (31) tiene un notable
parecido a la cualitativa los potenciales llegaron a través de los
experimentos de dispersión. Una característica inesperada de la
experimentación análisis de los datos fue la aparición de un
núcleo repulsiva de pequeño radio. El sistema recíproco, en la
Por otra parte, en realidad predice este núcleo repulsiva, es decir, V G3
. 6 Conclusiones Hagamos un resumen de lo más destacado. Después de
haber resuelto el enigma de la dualidad onda-partícula en una anterior
artículo 1 y entiende la legitimidad de la imagen de onda en la
teoría cuántica, el intento ha sido realizado para examinar la base
de su formalismo matemático con el beneficio de nuestro conocimiento de
la Sistema recíproco. Esto resultó productiva de dos maneras: en
primer lugar, se aclaró la situación en relación con la
Mecánica Cuántica, la identificación de algunos de sus errores
conceptuales. En segundo lugar se dio alcance a ampliar nuestro conocimiento
del sistema recíproco en forma de nuevas ideas que no hubieran sido
posible de otro modo. (I) Se encontró que las ecuaciones de
Schrödinger que haber reglas generales válidas para la
exploración de la funciones de onda en las distintas situaciones. (Ii) En
la región de espacio-tiempo, la velocidad puede ser vectorial (es decir,
''direccional'' en el contexto de la marco de tres dimensiones espaciales de
referencia), mientras que la velocidad inversa (como la energía) es
escalar. En
r) 4 + K G3 r 4 \ K I3 (31) Tomamos nota de que esto corresponde a lo que los
teóricos cuánticos convencionales llamarían la nuclear
potencial. Nuestro estudio indica que la ecuación (31) tiene un notable
parecido a la cualitativa los potenciales llegaron a través de los
experimentos de dispersión. Una característica inesperada de la
experimentación análisis de los datos fue la aparición de un
núcleo repulsiva de pequeño radio. El sistema recíproco, en la
Por otra parte, en realidad predice este núcleo repulsiva, es decir, V G3
. 6 Conclusiones Hagamos un resumen de lo más destacado. Después de
haber resuelto el enigma de la dualidad onda-partícula en una anterior
artículo 1 y entiende la legitimidad de la imagen de onda en la
teoría cuántica, el intento ha sido realizado para examinar la base
de su formalismo matemático con el beneficio de nuestro conocimiento de
la Sistema recíproco. Esto resultó productiva de dos maneras: en
primer lugar, se aclaró la situación en relación con la
Mecánica Cuántica, la identificación de algunos de sus errores
conceptuales. En segundo lugar se dio alcance a ampliar nuestro conocimiento
del sistema recíproco en forma de nuevas ideas que no hubieran sido
posible de otro modo. (I) Se encontró que las ecuaciones de
Schrödinger que haber reglas generales válidas para la
exploración de la funciones de onda en las distintas situaciones. (Ii) En
la región de espacio-tiempo, la velocidad puede ser vectorial (es decir,
''direccional'' en el contexto de la marco de tres dimensiones espaciales de
referencia), mientras que la velocidad inversa (como la energía) es
escalar. En
Página 15
Quantum Mechanics 15 la región de tiempo, la velocidad se encuentra para
ser escalar, mientras que la velocidad inversa es direccional-direccional en
las tres dimensiones del marco de referencia temporal. Variables de este
último tipo, por lo tanto, puede tomar valores intrínsecamente
negativos y ser representados por números complejos o cuaterniones como
sea el caso. (Iii) La penetración de la onda asociada con partículas
en las regiones de la energía cinética negativa resultantes de los
obstáculos potenciales de energía se encuentra que es un
fenómeno genuino región de tiempo. (Iv) En una línea similar,
se ha encontrado que la ocurrencia de una función de energía
potencial tipo bien en el región de tiempo conduce a la limitación
de los posibles valores de la energía total a un conjunto discreto. (V)
Un importante ley empírica como principio de exclusión de Pauli, que
no tiene teórico explicación en el contexto de la teoría
convencional, se podría entender fácilmente a partir de la
conocimiento de los puntos de referencia positivos y negativos sacado a la luz
por el recíproco Sistema. (Vi) Razonamiento a partir de los principios
del Sistema Recíproco la posible energía potencial funciones de la
región de tiempo relevante para los sistemas atómicos se
conjeturó. Mientras que evidencian una estrecha semejanza cualitativa a
los potenciales se han encontrado empíricamente, estudio más
detallado necesita para ser llevado a cabo para ver si conducen a la
predicción correcta de las propiedades relativas a espectroscopia, la
radiactividad y los experimentos de dispersión. En general parece que hay
una presunción en favor de la adopción de la Mecánica
Cuántica después purgarlo de sus errores conceptuales. Anexo I:
Relación de Euler A menudo, los cálculos se facilitan mediante la
adopción de funciones exponenciales con argumentos imaginarios en lugar
de las funciones seno o coseno, haciendo uso de las relaciones de Euler e Iowa
= Cos a + i sen A e - Ia = Cos a - i sin un que siguen directamente de la
serie de expansiones de estas funciones. Un número imaginario que
contiene, así como partes reales se llama un número complejo. Los
números complejos puede ser representada gráficamente en un sistema
de coordenadas rectangular, con la parte real correspondiente a el eje
horizontal y la parte imaginaria al eje vertical. Cualquier número
complejo puede entonces ser representada por un vector que se extiende desde
el origen e inclinada en un ángulo de la al eje real. Así A
 e i ? t representa un vector (radial) de la magnitud A que gira a la velocidad
angular ? (siendo t el tiempo). Se puede Debe observarse que cada una de las
relaciones inversas, pecar a = (E Iowa - E - Ia ) 2 i cos a = (E Iowa + E - Ia
) 2 representa un birotation.
e i ? t representa un vector (radial) de la magnitud A que gira a la velocidad
angular ? (siendo t el tiempo). Se puede Debe observarse que cada una de las
relaciones inversas, pecar a = (E Iowa - E - Ia ) 2 i cos a = (E Iowa + E - Ia
) 2 representa un birotation.
Página 16
16 Quantum Mechanics Apéndice II: La ecuación general de una onda de
velocidad constante Que una ola de forma arbitraria, pero que no cambia a
viajar en la dirección X de la referencia estacionaria marco XY a una
velocidad constante u. Esta ola aparece estacionario en un sistema de
referencia X 1 -Y 1 que se mueve a la misma velocidad u a lo largo de la
dirección X. Entonces podemos escribir x 1 = X - u
 t; y 1 = Y (32) Si la forma de onda en el marco co-móvil está dada
por y 1 = F (x 1 ), Tenemos que partir de la ecuación (1) y = f (x - u
t; y 1 = Y (32) Si la forma de onda en el marco co-móvil está dada
por y 1 = F (x 1 ), Tenemos que partir de la ecuación (1) y = f (x - u
 t) (33) Por la regla de la cadena de derivados que tenemos ? y ? x = dy dx 1 ?
x 1 ? x = dy dx 1
t) (33) Por la regla de la cadena de derivados que tenemos ? y ? x = dy dx 1 ?
x 1 ? x = dy dx 1
 1, ? y ? x = dy dx 1 ? x 1 ? x = dy dx 1
1, ? y ? x = dy dx 1 ? x 1 ? x = dy dx 1
 (- u). Por lo tanto la relación entre los dos derivados es ? y ? x = - 1
u
(- u). Por lo tanto la relación entre los dos derivados es ? y ? x = - 1
u
 ? y ? t (34) Del mismo modo para una onda que viaja en la dirección X se
obtiene ? y ? x = + 1 u
? y ? t (34) Del mismo modo para una onda que viaja en la dirección X se
obtiene ? y ? x = + 1 u
 ? y ? t (35) Ahora, una aplicación repetida de los rendimientos
procedimiento anterior ? 2 y ? x 2 = 1 u 2
? y ? t (35) Ahora, una aplicación repetida de los rendimientos
procedimiento anterior ? 2 y ? x 2 = 1 u 2
 ? 2 y ? t 2 (36) que es la ecuación de gobierno de la función de
onda, y es la misma para las ondas que viajan en cualquiera
? 2 y ? t 2 (36) que es la ecuación de gobierno de la función de
onda, y es la misma para las ondas que viajan en cualquiera
--------------------------------------------------------------------------------------
3.2 Explicación de los estados de energía negativa
Cuando nos dirigimos al Sistema
Recíproca para obtener una explicación de la posibilidad de la
existencia de estados de energía negativa, lo que encontramos es el
siguiente. En la región de espacio-tiempo, es decir, en el contexto de la
sistema de referencia espacial tridimensional, velocidad (espacio / tiempo) es
vectorial, es decir, puede tener sentido en espacio, por lo que podría
tomar valores positivos o negativos. Esto es porque en este caso el espacio es
tridimensional y el tiempo es escalar. En este marco, la energía, la cual
es la velocidad inversa unidimensional (Tiempo / espacio), es escalar, y puede
tomar únicamente en valores de cero o positivo. Por otra parte, la
región de tiempo es un dominio de la trama de referencia temporal en tres
dimensiones. En este caso el tiempo es de tres dimensiones y el espacio es
escalar. Por consiguiente, la velocidad inversa (es decir, la energía) es
la cantidad que es ''Direccional'', es decir, puede tomar una ''dirección
temporal'' en el contexto de las tres dimensiones marco de referencia
temporal. Por lo tanto, es perfectamente posible para que tome en valores
negativos también. (Se debe ser advertido de que ''la dirección en
el tiempo'' no tiene nada que ver con la dirección en el espacio, sino
que ha de ser entendimos que sólo estamos hablando metafóricamente.)
Además, en la región de tiempo, la velocidad es la cantidad que es
escalar, siendo un ejemplo la velocidad de desplazamiento total neto del
átomo, a saber, la atómica número Z. Por otra parte la
posibilidad de que incluso la energía potencial (siendo una velocidad
inversa) podría ser ''direccional'' en el tiempo en tres dimensiones, y
por lo tanto estar representado por números complejos en la región
de tiempo, no puede pasarse por alto. De hecho, los teóricos
cuánticos resulta necesario adoptar el complejo potencial
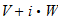 en lugar de la
en lugar de la
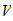 en la teoría de la dispersión. Aquí el número de onda
en la teoría de la dispersión. Aquí el número de onda
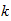 se vuelve compleja y se escribe como
se vuelve compleja y se escribe como
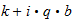 de La ecuación (20) se convierte en
de La ecuación (20) se convierte en
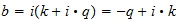 ,
y tenemos
,
y tenemos
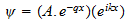 (21) Al
mismo tiempo podemos ver que se trata de la función de onda de una onda
de cuya amplitud disminuye a medida que avances, y por lo tanto representa un
haz de partículas algunas de las cuales están siendo absorbidos.
(21) Al
mismo tiempo podemos ver que se trata de la función de onda de una onda
de cuya amplitud disminuye a medida que avances, y por lo tanto representa un
haz de partículas algunas de las cuales están siendo absorbidos.
3.2 Explanation of the Negative Energy States
When we turn to the Reciprocal System for an explanation of the possibility of the existence of negative energy states, what we find is as follows. In the time-space region, that is, in the context of the three-dimensional spatial reference frame, speed (space/time) is vectorial, that is, can have direction in space and therefore could take on positive or negative values. This is because in this case space is three-dimensional and time is scalar. In this frame, energy, which is one-dimensional inverse speed (time/space), is scalar, and can take on zero or positive values only. On the other hand, the time region is a domain of the three-dimensional temporal reference frame. In this case time is three-dimensional and space is scalar. Consequently the inverse speed (namely, energy) is the quantity that is directional, that is, can take on a temporal direction in the context of the three-dimensional temporal reference frame. Therefore it is perfectly possible for it to take on negative values as well. (It must be cautioned that direction in time has nothing to do with direction in space; it is to be understood that we are only speaking metaphorically.) Further, in the time region, speed is the quantity that is scalar, an example being the net total speed displacement of the atom, namely, the atomic number Z.
Moreover the possibility that even potential energy (being an inverse speed)
could be directional in the three-dimensional time, and hence be represented
by complex numbers in the time region, cannot be overlooked. Indeed the
Quantum theorists find it necessary to adopt the complex potential
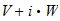 in place of
in place of
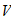 in scattering theory. Here the wave number
in scattering theory. Here the wave number
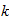 becomes complex and is written as
becomes complex and is written as
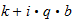 of Equation (20) becomes
of Equation (20) becomes
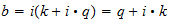 ,
and we have
,
and we have
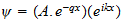 (21)
(21)
We can at once see that this is the wave function of a traveling wave of whose amplitude decreases as it advances, and therefore represents a beam of particles some of which are getting absorbed.
---------------------------------------------------------------------------
Small errors in nomenclature KVK Quantum Mechanic Nehru, reciprocal system
Quantum Mechanics
2.1 Radiation Waves
says
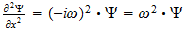
should say (9)
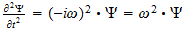
Francisco Cabot Pol / Orene.org